cyphen156
알고리듬#1 최대공약수와 최소공배수 : 유클리드 알고리즘 본문
흔히 유클리드 호제법(Euclidean algorithm)으로 알려진 두 양의 정수의 최대공약수와 최소공배수를 빠르게 찾아내는 문제해결방법이다.

수식이 조금 난잡해서 보기 불편한데 함수 수식으로 변환하면 f(x) = ax + b가 성립한다면 gcd(a, b) = gcd(r, b)이다
GDC(greatest common divisor/최대공약수)
최대공약수를 구하는 일반적인 방법은 다음과 같다.
두 수를 소인수 분해하여 서로 공통되는 약수들을 찾아 모두 곱한다.
A = 100, B = 12일 때
두 수의 약수들은 각각 (1, 2, 4, 5, 10, 20, 25, 50, 100), (1, 2, 3, 4, 6, 12)로 1 * 2 * 4 = 8이다.
코드로 약수를 찾아가는 과정은 다음과 같다
아래의 코드는 한 정수의 모든 약수를 찾아내기 때문에 시간복잡도가 O(N)으로 input의 크기에 비례한다.
// 일반적인 방법
// 시간복잡도 O(N)
int findDivisor(int A){
int i = 1;
while(i <= A) {
if(A % i == 0) {
printf("%d ", i);
}
i++;
}
}이것을 조금 더 줄이면 약수는 항상 배수로 존재하기 때문에 input의 절반까지만 확인해도 된다는 것이 있다.
하지만 시간복잡도는 항상 상수배는 무시하기 때문에 여전히 O(N)으로 표기한다.
// 일반적인 방법의 연산횟수 1/2
// 시간복잡도 O(N)
int findDivisor(int A){
int i = 1;
while(i <= A/2) {
if(A % i == 0) {
printf("%d ", i);
}
i++;
}
}조금더 나아가면 절반이 아니라 제곱근 까지만 연산하면 된다는 것을 깨닫게 된다. 그 이유는 10000의 예시를 확인하면 알 수 있다. 약수는 항상 대칭을 이루기 때문에 100 * 100까지만 찾아낸다면 다른 약수들은 이미 찾은것이나 마찬가지이기 때문이다.
// input의 약수를 찾는 방법 #3 제곱근까지만 확인하기
// 시간복잡도 O(sqrt(N))
int findDivisor_Root(int A) {
int i;
for (i = 1; i <= sqrt(A); i++)
{
if (A % i == 0)
{
printf("%d ", i);
if (i != A / i) // 약수 쌍 출력
{
printf("%d ", A / i);
}
}
}
return 0;
}여기까지 왔다면 시간복잡도를 많이 줄였다 하지만 최대공약수를 찾는다면 이 과정의 두 배가 걸린다.
이 시간마저 부족하다고 느껴질 때 사용하는 효율적인 알고리즘이 유클리드 호제법이다.
유클리드 호제법
큰 수를 작은수로 나누는 것을 나머지가 0이 될 때까지 반복하고 마지막 연산의 작은 수가 바로 최대공약수라는 것이다.
어떻게 이것이 가능하냐? 하신다면 두 수 중 큰 수를 작은 수로 나누었을 때 나머지가 존재하지 않는다면 해당 수가 최대 공약수임을 증명하고, 만약 존재한다면 더 작은 수인 최대 공약수가 존재한다는 것이기 때문이다.
그렇기 때문에 유클리드 호제법은 시간복잡도가 O(logN)이다.
만약 A가 100, B가 12 일 때 GCD는
1회 반복시 A = 100, B = 12 ... C = 4 (100%12)
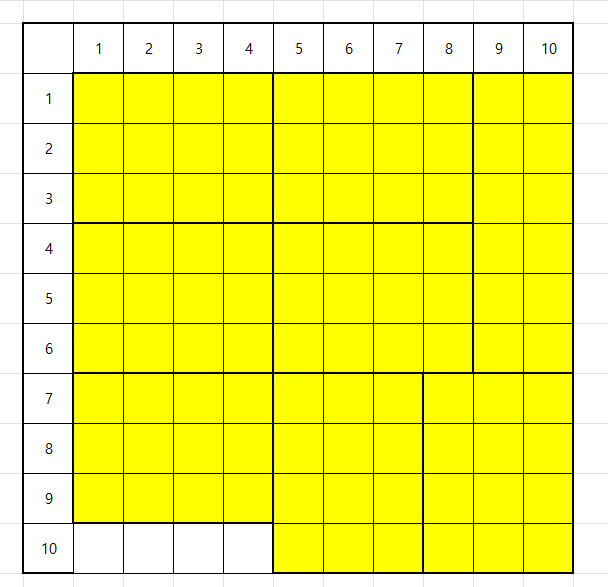
2회 반복시 A = 12, B = 4 ... C = 0
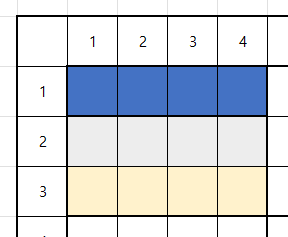
100과 12의 최대공약수는 4 * 25 / 4 * 3 이므로 4가 된다.
유사 코드
GDC:
int input A, B (A, B > 0)
int C
while(B != 0) {
C = A % B; B가 0이 되면, A는 최대공약수(GCD)입니다.
A = B;
B = C;
}
restul = A;C코드
int GCD(int A, int B) {
int C;
while(B != 0) {
C = A % B;
A = B;
B = C;
}
return A;
}LCM(least common multiple/최소공배수)
유클리드 호제법을 응용한다면 최소공배수 또한 빠르게 구할 수 있다.
이것은 두 양의 정수의 약수들의 곱이 최소공배수를 형성하는데 두 수를 곱한 뒤 최대공약수를 나눠주면 된다.
이것이 가능해지는 이유는 두 수를 곱한 것이 약수들의 곱에 최대공약수를 한번 더 곱한 것이 결과로 나타나기 때문이다.
만약 A가 12, B가 8 일 때 두 수의 약수는 각각 (3, 4), (2, 4)이다 여기서 최소 공배수는 2 * 3 * 4이므로 24가 나와야 한다.
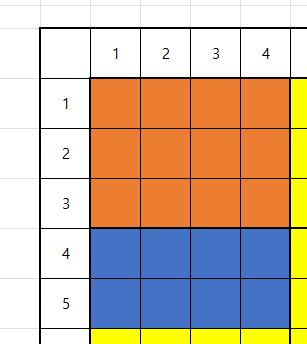
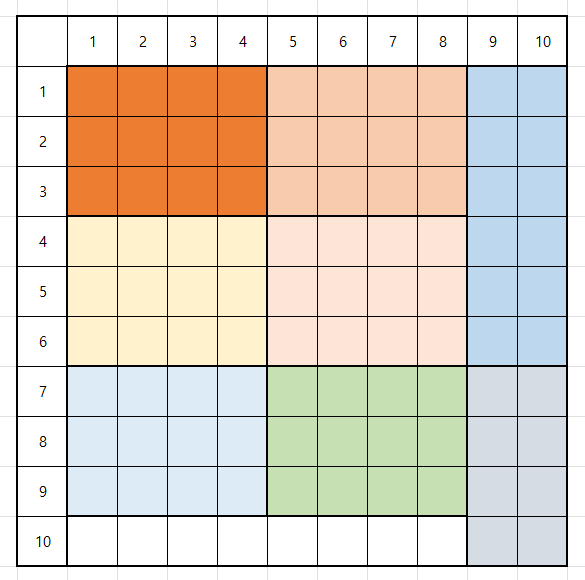
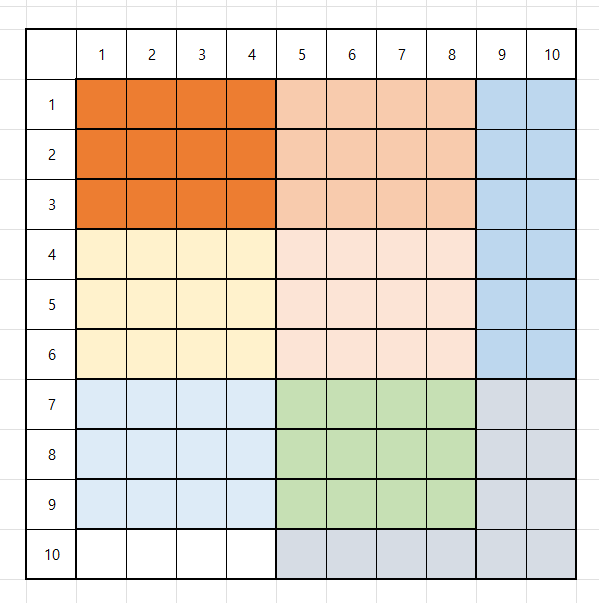
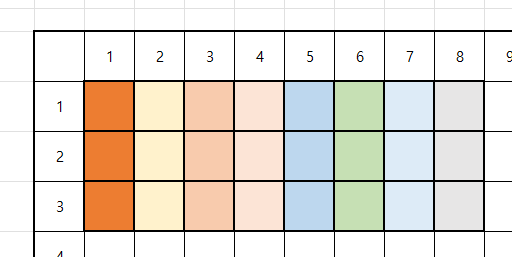
유사 코드
LCM:
int input A, B, C (A, B > 0, C = GCD)
int result
result = A * B / CC코드
int LCM(int A, int B, int GCD) {
int result;
result = A * B / GCD;
return result;
}최대공약수와 최소공배수를 어디에 써먹을까 하는데 지금 딱 생각나는것은 통계 추정 분야와 딥러닝이다.
둘 모두 어떤 데이터들로부터 공통점을 찾고, 이를 활용할 때 사용하는 것 같다.
다음은 GPT에게 물어본 사용처이다.
최대공약수(GCD)와 최소공배수(LCM)의 개념은 수학과 컴퓨터 과학에서 널리 사용되며, 그 용도는 다양합니다. 통계 추정과 딥러닝을 포함한 여러 분야에서 이러한 개념들이 응용될 수 있는 방법을 살펴보겠습니다.
통계 추정
통계 추정에서 GCD와 LCM이 직접적으로 적용되는 예는 드물지만, 이 개념들은 데이터의 패턴을 분석하거나 데이터 세트 간의 관계를 이해하는 데 간접적으로 유용할 수 있습니다. 예를 들어, 시간 간격이나 샘플링 빈도와 같은 데이터의 주기성을 분석할 때 최대공약수를 사용하여 공통 패턴이나 주기를 찾아낼 수 있습니다. 또한, 여러 변수 또는 측정치 간의 관계를 분석할 때 LCM을 활용하여 데이터 포인트를 동기화하거나 통합하는 방법을 고려할 수 있습니다.
딥러닝
딥러닝에서는 GCD와 LCM이 직접적으로 적용되는 경우보다는, 이 개념들이 알고리즘의 효율성을 높이거나 네트워크 아키텍처를 설계하는 데 도움을 줄 수 있습니다.
- 배치 사이즈 최적화: 딥러닝 모델을 훈련시킬 때, 배치 사이즈의 선택은 메모리 사용량과 계산 효율성에 큰 영향을 미칩니다. GCD와 LCM을 사용하여 데이터 세트의 크기와 가장 잘 맞는 배치 사이즈를 결정함으로써 GPU 메모리 사용을 최적화하고 병렬 처리 효율성을 높일 수 있습니다.
- 네트워크 아키텍처 설계: 특정한 구조의 네트워크에서, 예를 들어 컨볼루션 신경망(CNN)에서 필터의 크기나 스트라이드 설정을 결정할 때, GCD와 LCM 개념을 활용하여 입력 데이터와 필터 간의 호환성을 높이고 효율적인 정보 추출을 도모할 수 있습니다.
- 데이터 전처리: 여러 소스에서 수집한 데이터 세트를 결합할 때, GCD나 LCM을 이용하여 데이터 포인트 간의 최소 간격을 결정하거나 동기화할 수 있습니다. 이를 통해 불규칙한 간격의 시계열 데이터를 균일하게 만들거나, 여러 센서에서 수집한 데이터를 통합할 때 유용할 수 있습니다.
GCD와 LCM은 이처럼 다양한 방식으로 응용 프로그램의 설계나 데이터 분석 과정에서 유용하게 활용될 수 있습니다. 이 개념들을 활용하는 것은 종종 간접적이며, 구체적인 문제 해결 과정에서 창의적인 접근 방식을 필요로 합니다.
해당 코드들은 제 깃허브에 있습니다. 유사코드는 제공하지 않습니다.
Workspace/알고리듬 at main · cyphen156/Workspace · GitHub
'컴퓨터공학 > 알고리듬' 카테고리의 다른 글
| 알고리듬#2 소수판정법(primarity Test) (1) | 2024.02.19 |
|---|---|
| 알고리듬#1+@ 이진 최대공약수(스테인의 알고리듬) (0) | 2024.02.15 |
| Chapter1 알고리즘 개요 (0) | 2022.09.16 |



