게임 수학 8장 : 삼각형(물체를 구성하는 가장 작은 단위)-메시와 텍스쳐

Notice

Recent Posts

Recent Comments

Link

« 2025/04 »
일	월	화	수	목	금	토
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

Today

Total

Archives

Tags more

관리 메뉴

cyphen156

게임 수학 8장 : 삼각형(물체를 구성하는 가장 작은 단위)-메시와 텍스쳐 본문

수학/게임수학

게임 수학 8장 : 삼각형(물체를 구성하는 가장 작은 단위)-메시와 텍스쳐

cyphen156 2025. 3. 19. 20:01

이전까지는 한 점(점의 좌표) 혹은 두 점(선분, 벡터) 에 대해 공부했다면, 이제부터는 3D 그래픽스 및 게임 그래픽에서 가장 기본적인 단위인 세 개의 점(정점, Vertex)으로 구성된 삼각형에 대해서 배우겠다.

정점(Vertex), 삼각형(Triangle), 폴리곤(Polygon)

앞선 장에서 두 벡터가 서로 선형 독립의 관계라면 같은 차원 내의 공간상에서 어떠한 벡터든 만들어 낼 수 있다고 배웠다.

그런데 아핀 공간상에서 점들의 결합의 스칼라 결과는 항상 1이 되어야 한다고 했다.

또한 선분을 그릴 때 S와 T값을 [0, 1]로고정한다면 유한한 크기의 직선을 구할 수 있다고 했다.

이것을 통해 삼각형의 형태 안에 존재하는 점들이 모두 아핀 결합식으로 생성될 수 있는 점들이라 판단할 수 있다.

이렇게 탄생한 삼각형의 영역을 컨벡스 영역(Convex region)^[각주:1]이라고 한다.

이와는 반대로 영역 밖을 지나가는 부분이 있는 선분은 컨케이브 영역이다.

그런데 만약 각 점들의 비율이 각각 약 0.33/0.33/0.33으로 동일 하다면 세 점들의 아핀 결합의 결과가 삼각형의 중점 좌표를 나타냄 또한 알 수 있게 된다.

여기서 한단계 더 나아가 보자 만약 네 점들의 아핀 결합을 표현한다면 어떻게 될까? 앞서 두 점에서 세 점의 결합과 더불어 표현 범위의 제한으로 점이 하나 늘어날 수록 표현할 수 있는 공간이 한 차원 늘어난 다는 것을 알았다. 그렇다면 네 점의 아핀 결합에서는 2차원 평면 도형에서 3차원 입체 도형으로 나타날 것이다.

그렇기 때문에 네 점의 아핀 결합은 삼각 뿔의 형태를 띄게 된다.

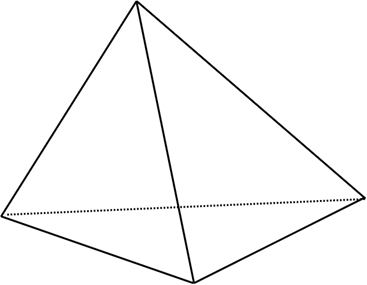
정점(Vertex)과 메시(Mesh)

앞서서 점들의 결합을 통해 입체 도형을 3차원 공간에서 표현한다고 했다.

이 점들에 대한 위치, 색상, 방향, 법선(Normal), 텍스처 좌표(Texture Coordinate), 가중치(Weight) 등 과 같은 다양한 부가 정보들을 함께 모아 하나의 자료형으로 묶어서 관리하는 것을 정점이라 부른다.

그리고 이 정점들에서 가져온 데이터들을 통해 입체적인 사물을 그리기 위하여 사물의 표면을 삼각형들의 결합으로 표현한 것을 메시라고 한다.

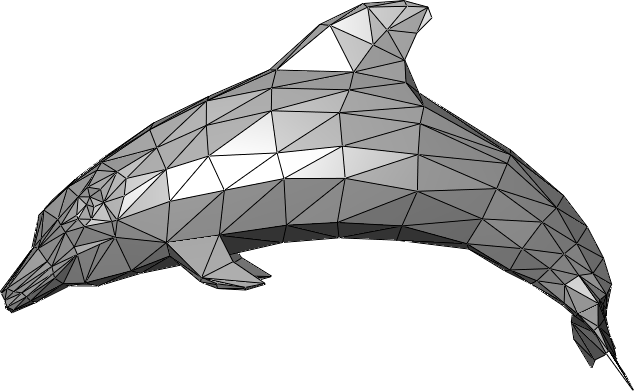
정점버퍼와 인덱스 버퍼

물체를 자세하게 표현하려 할 수록 정점과 메시 정보가 기하급수적으로 많아진다.

당장 삼각 뿔 하나만 그린다 하더라도 1개의 입체도형을 그리기 위해 4개의 메시와 각 메시에 연결된 정점데이터가 3개씩 12개, 총 17개의 개별 데이터가 필요하다. 하지만 실제로 각 메시들이 연결되어 있기 때문에 중복되는 정점 데이터는 재활용 할 수 있다고 판단하면 정점 데이터의 수는 4개로 줄어들게 되긴 하지만 역시 많은 메모리를 사용하게 된다는 것에는 틀림 없다.

이러한 많은 데이터를 빠르고 쉽게 가져와 사용하기 위해 메모리상에 점에 대한 위치만을 기록한 별도의 배열로 만들어 관리하는데 이것을 정점 버퍼와 인덱스 버퍼라고 한다.

정점 버퍼(VBO): 정점의 좌표, 색상, 텍스처 좌표 등의 정보를 저장.
인덱스 버퍼(IBO): 정점의 순서 정보를 저장하여, 중복되는 정점을 재사용할 수 있도록 최적화.

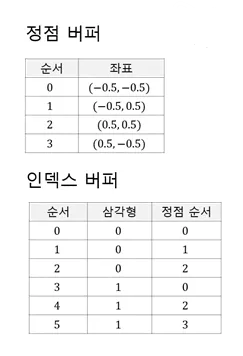
와이어 프레임

정점 버퍼와 인덱스 버퍼에 표시된 점들을 서로 연결하여 선분만을 그려 메시를 형상화하여 표현한 것을 와이어 프레임이라고 한다.

와이어 프레임으로 렌더링 했을 때의 장점은 간단한 로직을 통해 선분만을 그리기 때문에 빠른 렌더링이 가능하다는 것이고, 이것이 디버깅 할때 불필요한 정보들을 떼어내고 빌드하는 일종의 프로토타이핑 기법이라고 볼 수 있다.

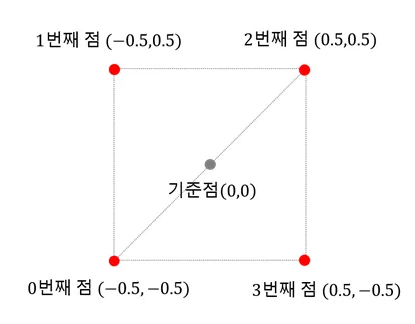
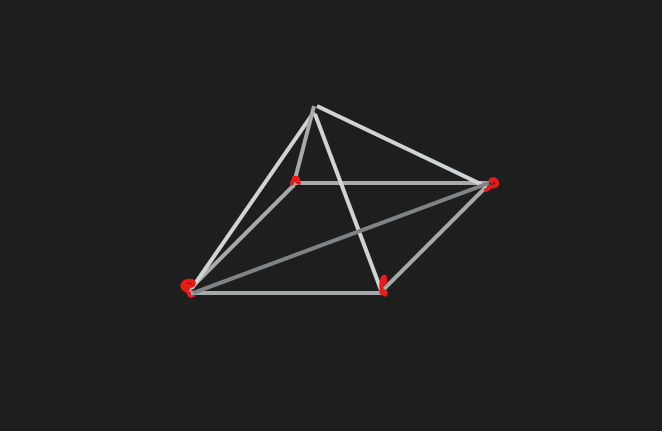
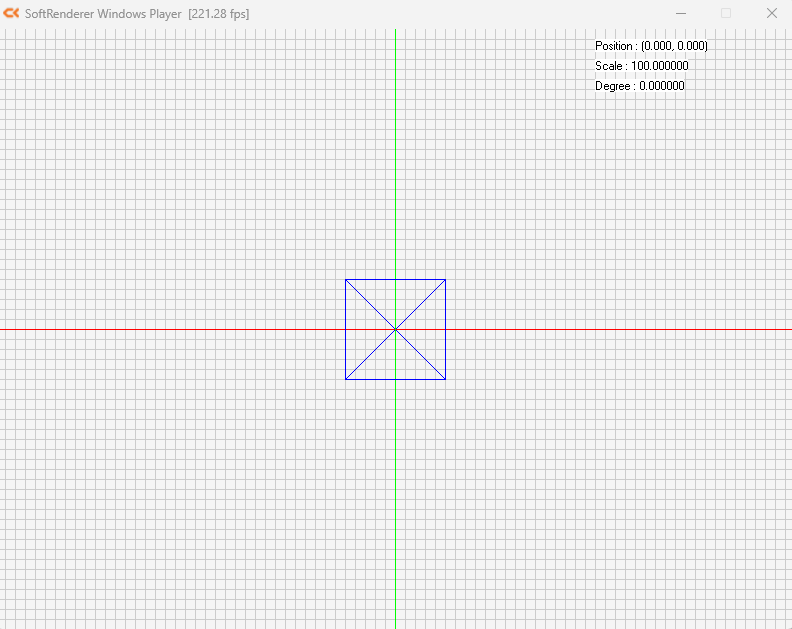
네 점으로 이루어진 2차원 와이어 프레임 도형과 다섯 개의 점으로 이루어진 3차원 와이어프레임 도형

예제 8_1 5개의 정점과 4개의 삼각형 2차원 와이어 프레임 도형렌더링

Render2D함수

/// 예제 8_1 5개의 정점과 4개의 삼각형 2차원 와이어 프레임 도형렌더링
static constexpr float squareHalfSize = 0.5f;
static constexpr size_t vertexCount = 5;
static constexpr size_t triangleCount = 4;

// 메시를 구성하는 정점 배열과 인덱스 배열의 생성
static constexpr std::array<Vertex2D, vertexCount> rawVertices =
{
	Vertex2D(Vector2(-squareHalfSize, -squareHalfSize)),	//	-0.5, -0.5
	Vertex2D(Vector2(-squareHalfSize, squareHalfSize)),		//	-0.5, 0.5
	Vertex2D(Vector2(squareHalfSize, squareHalfSize)),		//	0.5, 0.5
	Vertex2D(Vector2(squareHalfSize, -squareHalfSize)),		//	0.5, -0.5
	Vertex2D(Vector2(0, 0)),								//	0, 0
};

static constexpr std::array<size_t, triangleCount * 3> indices =
{
	0, 1, 4,
	1, 2, 4,
	2, 3, 4,
	0, 3, 4
};
// 행렬을 적용한 메시 정보를 사용해 물체를 렌더링
static std::vector<Vertex2D> vertices(vertexCount);
for (size_t vi = 0; vi < vertexCount; ++vi)
{
	vertices[vi].Position = finalMatrix * rawVertices[vi].Position;
}

// 변환된 정점을 잇는 선 그리기
for (size_t ti = 0; ti < triangleCount; ++ti)
{
	size_t bi = ti * 3;
	r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 1]].Position, _WireframeColor);
	r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 2]].Position, _WireframeColor);
	r.DrawLine(vertices[indices[bi + 1]].Position, vertices[indices[bi + 2]].Position, _WireframeColor);
}

무게 중심 좌표

컨벡스 공간 내에 생성될 수 있는 좌표들은 모두 메시의 구성원이라고 판단 할 수 있다.

앞서 아핀 결합식에서 세 계수를 조합해 (s, t, 1-s-t) 생성한 좌표를 무게중심좌표라 부르며 , 각 정점들의 가중치를 동일하게 준다면 물체의 중점 좌표를 구할 수 있다.

반대로 컨벡스 공간에서 벗어나는 좌표들은 모두 메시에 포함되지 않는 정보라 판단 할 수 있다.

이 정보들을 가지고 삼각형을 그려보겠다.

삼각형 색칠하기

좌표 공간 내에서 우선 선을 그리고 그 안을 모두 색칠해야 한다.

이것을 2D 가상 공간 내에 그리려면 삼각형을 포함하는 픽셀영역을 구한 뒤, 각 픽셀들을 순회 하면서 해당 점이 컨벡스 공간 내에 있는지를 판단해야 한다. 이 때 분모 값은 상수이기 때문에 변하지 않는다.

그리고 분모의 계산 값이 0이라면 수식이 성립되지 않으므로 건너뛰어 최적화 할 수 있을 것이다.

이번 예제는 8_1을 재활용 하도록 한다.

예제 8_2-8_1영역색칠하기

변환된 정점을 잇는 선 그리기에서 이어 합니다.

이전에 그렸던 선분을 가장 마지막에 그려야 포인트 그릴때 덮어씌워 선을 그립니다.

// 변환된 정점을 잇는 선 그리기
for (size_t ti = 0; ti < triangleCount; ++ti)
{
	size_t bi = ti * 3;
	
	/// 예제 8_2-8_1영역 색칠하기 
	std::array<Vertex2D, 3> tv = {
		vertices[indices[bi]], vertices[indices[bi + 1]], vertices[indices[bi + 2]]};

	Vector2 minPos(Math::Min3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
		Math::Min3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));
	Vector2 maxPos(Math::Max3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
		Math::Max3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));

	// 무게 중심좌표를 위한 준비작업
	Vector2 u = tv[1].Position - tv[0].Position;
	Vector2 v = tv[2].Position - tv[0].Position;

	// 공통 분모 ( uu * vv - uv * uv )
	float udotv = u.Dot(v);
	float vdotv = v.Dot(v);
	float udotu = u.Dot(u);
	float denominator = udotv * udotv - vdotv * udotu;

	// 퇴화삼각형은 그리지 않음
	if (denominator == 0.0f)
	{
		continue;
	}

	float invDenominator = 1.f / denominator;
	// 화면상의 점 구하기
	ScreenPoint lowerLeftPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, minPos);
	ScreenPoint upperRightPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, maxPos);

	// 두 점이 화면 밖을 벗어나는 경우 클리핑 처리
	lowerLeftPoint.X = Math::Max(0, lowerLeftPoint.X);
	lowerLeftPoint.Y = Math::Min(_ScreenSize.Y, lowerLeftPoint.Y);
	upperRightPoint.X = Math::Min(_ScreenSize.X, upperRightPoint.X);
	upperRightPoint.Y = Math::Max(0, upperRightPoint.Y);

	// 삼각형을 둘러싼 사각형 영역의 픽셀을 모두 순회
	for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
	{
		for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
		{
			ScreenPoint fragment = ScreenPoint(x, y);
			Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
			Vector2 w = pointToTest - tv[0].Position;
			float wdotu = w.Dot(u);
			float wdotv = w.Dot(v);

			// 분자 값을 구하고 최종 무게중심좌표 산출
			float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
			float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
			float oneMinusST = 1.f - s - t;

			// 컨벡스 조건을 만족할 때만 점 찍기
			if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
			{
				r.DrawPoint(fragment, LinearColor::Red);
			}
		}
	}

	r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 1]].Position, LinearColor::Black);
	r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 2]].Position, LinearColor::Black);
	r.DrawLine(vertices[indices[bi + 1]].Position, vertices[indices[bi + 2]].Position, LinearColor::Black);

}

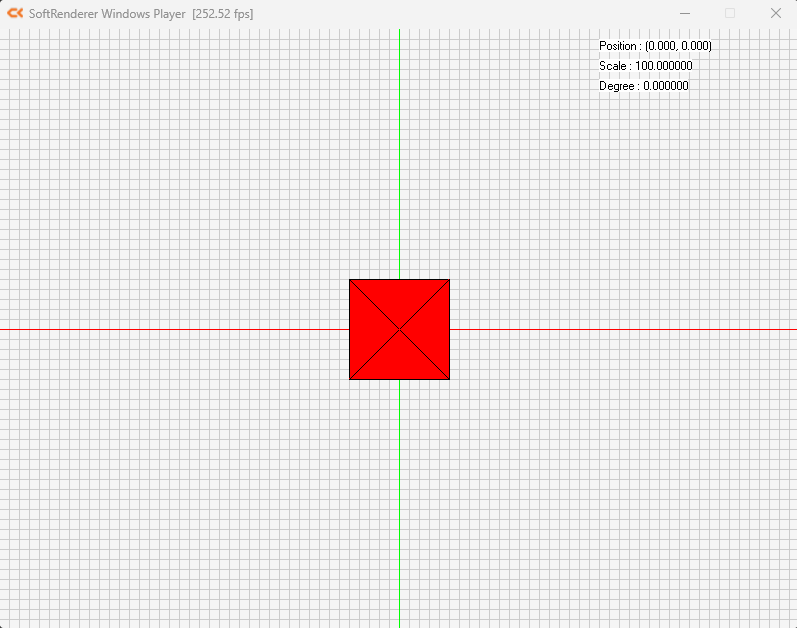
여태까지 우리는 컨벡스 영역을 특정한 색으로 색칠했다.

사실 정점(버텍스)는 좌표 말고도 다른 많은 정보들 또한 포함하고 있는 자료라고 말했다.

이제 우리는 버텍스에 저장된 색상정보를 활용할 수 있다.

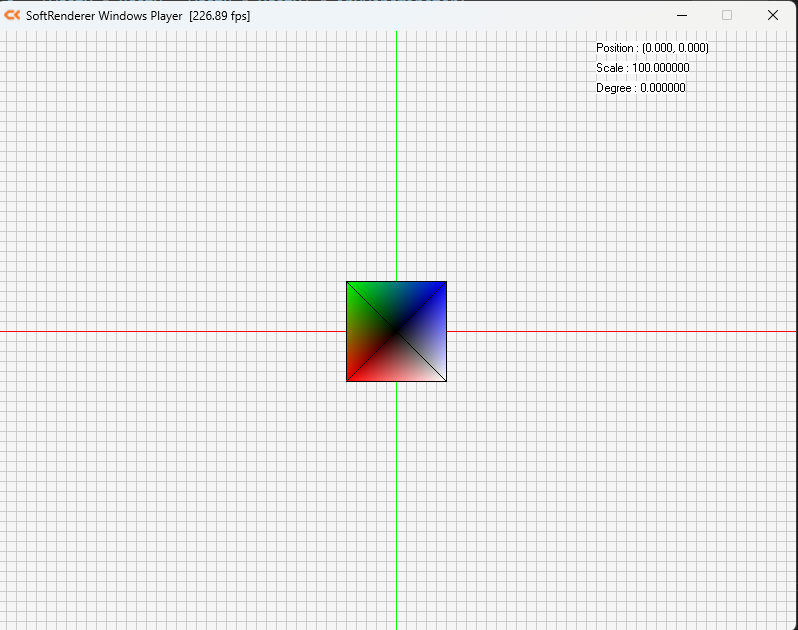
예제 8_3 사각형 버텍스 정보로 색칠하기

정점 버퍼에 색상 정보를 포함시고, 색상 조합을 선택할 때 이 것을 활용하는 작업을 하겠다.

이를 위해 rawVertices 변수에 색상 정보를 RGB 순으로 추가 입력하도록 하겠다.

// 메시를 구성하는 정점 배열
static constexpr std::array<Vertex2D, vertexCount> rawVertices =
{
	//	-0.5, -0.5,	/	Red
	//	-0.5, 0.5	/	Green
	//	0.5, 0.5	/	Blue
	//	0.5, -0.5	/	White
	//	0, 0		/	Black
	Vertex2D(Vector2(-squareHalfSize, -squareHalfSize), LinearColor(1.f, 0.f, 0.f)), 	
	Vertex2D(Vector2(-squareHalfSize, squareHalfSize), LinearColor(0.f, 1.f, 0.f)),		
	Vertex2D(Vector2(squareHalfSize, squareHalfSize), LinearColor(0.f, 0.f, 1.f)),		
	Vertex2D(Vector2(squareHalfSize, -squareHalfSize), LinearColor(1.f, 1.f, 1.f)),		
	Vertex2D(Vector2(0, 0), LinearColor(0.f, 0.f, 0.f)),								
};

// 행렬을 적용한 메시 정보를 사용해 물체를 렌더링
static std::vector<Vertex2D> vertices(vertexCount);
for (size_t vi = 0; vi < vertexCount; ++vi)
{
	vertices[vi].Position = finalMatrix * rawVertices[vi].Position;
	vertices[vi].Color = rawVertices[vi].Color;
}

// 컨벡스 조건을 만족할 때만 점 찍기
if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
{
				LinearColor outColor = tv[0].Color * oneMinusST + tv[1].Color * s + tv[2].Color * t;
				r.DrawPoint(fragment, outColor);
}

예제 8_3의 최종 코드는 다음과 같다.

#include "Precompiled.h"
#include "SoftRenderer.h"
#include <random>
using namespace CK::DD;

// 격자를 그리는 함수
void SoftRenderer::DrawGizmo2D()
{
	auto& r = GetRenderer();
	const auto& g = Get2DGameEngine();

	// 그리드 색상
	LinearColor gridColor(LinearColor(0.8f, 0.8f, 0.8f, 0.3f));

	// 뷰의 영역 계산
	Vector2 viewPos = g.GetMainCamera().GetTransform().GetPosition();
	Vector2 extent = Vector2(_ScreenSize.X * 0.5f, _ScreenSize.Y * 0.5f);

	// 좌측 하단에서부터 격자 그리기
	int xGridCount = _ScreenSize.X / _Grid2DUnit;
	int yGridCount = _ScreenSize.Y / _Grid2DUnit;

	// 그리드가 시작되는 좌하단 좌표 값 계산
	Vector2 minPos = viewPos - extent;
	Vector2 minGridPos = Vector2(ceilf(minPos.X / (float)_Grid2DUnit), ceilf(minPos.Y / (float)_Grid2DUnit)) * (float)_Grid2DUnit;
	ScreenPoint gridBottomLeft = ScreenPoint::ToScreenCoordinate(_ScreenSize, minGridPos - viewPos);

	for (int ix = 0; ix < xGridCount; ++ix)
	{
		r.DrawFullVerticalLine(gridBottomLeft.X + ix * _Grid2DUnit, gridColor);
	}

	for (int iy = 0; iy < yGridCount; ++iy)
	{
		r.DrawFullHorizontalLine(gridBottomLeft.Y - iy * _Grid2DUnit, gridColor);
	}

	ScreenPoint worldOrigin = ScreenPoint::ToScreenCoordinate(_ScreenSize, -viewPos);
	r.DrawFullHorizontalLine(worldOrigin.Y, LinearColor::Red);
	r.DrawFullVerticalLine(worldOrigin.X, LinearColor::Green);

}

// 게임 오브젝트 목록


// 최초 씬 로딩을 담당하는 함수
void SoftRenderer::LoadScene2D()
{
	// 최초 씬 로딩에서 사용하는 모듈 내 주요 레퍼런스
	auto& g = Get2DGameEngine();

}

// 게임 로직과 렌더링 로직이 공유하는 변수
Vector2 currentPosition;
float currentScale = 100.f;
float currentDegree = 0.f;

// 게임 로직을 담당하는 함수
void SoftRenderer::Update2D(float InDeltaSeconds)
{
	// 게임 로직에서 사용하는 모듈 내 주요 레퍼런스
	auto& g = Get2DGameEngine();
	const InputManager& input = g.GetInputManager();

	// 게임 로직의 로컬 변수
	static float moveSpeed = 100.f;
	static float scaleMin = 50.f;
	static float scaleMax = 200.f;
	static float scaleSpeed = 100.f;
	static float rotateSpeed = 180.f;

	Vector2 inputVector = Vector2(input.GetAxis(InputAxis::XAxis), input.GetAxis(InputAxis::YAxis)).GetNormalize();
	Vector2 deltaPosition = inputVector * moveSpeed * InDeltaSeconds;
	float deltaScale = input.GetAxis(InputAxis::ZAxis) * scaleSpeed * InDeltaSeconds;
	float deltaDegree = input.GetAxis(InputAxis::WAxis) * rotateSpeed * InDeltaSeconds;

	// 물체의 최종 상태 설정
	currentPosition += deltaPosition;
	currentScale = Math::Clamp(currentScale + deltaScale, scaleMin, scaleMax);
	currentDegree += deltaDegree;
}

// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render2D()
{
	// 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
	auto& r = GetRenderer();
	const auto& g = Get2DGameEngine();

	// 배경에 격자 그리기
	DrawGizmo2D();

	// 메시 데이터의 선언


	// 아핀 변환 행렬 ( 크기 ) 
	Vector3 sBasis1(currentScale, 0.f, 0.f);
	Vector3 sBasis2(0.f, currentScale, 0.f);
	Vector3 sBasis3 = Vector3::UnitZ;
	Matrix3x3 sMatrix(sBasis1, sBasis2, sBasis3);

	// 아핀 변환 행렬 ( 회전 ) 
	float sin = 0.f, cos = 0.f;
	Math::GetSinCos(sin, cos, currentDegree);
	Vector3 rBasis1(cos, sin, 0.f);
	Vector3 rBasis2(-sin, cos, 0.f);
	Vector3 rBasis3 = Vector3::UnitZ;
	Matrix3x3 rMatrix(rBasis1, rBasis2, rBasis3);

	// 아핀 변환 행렬 ( 이동 ) 
	Vector3 tBasis1 = Vector3::UnitX;
	Vector3 tBasis2 = Vector3::UnitY;
	Vector3 tBasis3(currentPosition.X, currentPosition.Y, 1.f);
	Matrix3x3 tMatrix(tBasis1, tBasis2, tBasis3);

	// 모든 아핀 변환을 곱한 합성 행렬. 크기-회전-이동 순으로 적용
	Matrix3x3 finalMatrix = tMatrix * rMatrix * sMatrix;

	// 현재 위치, 크기, 각도를 화면에 출력
	r.PushStatisticText(std::string("Position : ") + currentPosition.ToString());
	r.PushStatisticText(std::string("Scale : ") + std::to_string(currentScale));
	r.PushStatisticText(std::string("Degree : ") + std::to_string(currentDegree));
	
	/// 예제 8_1 5개의 정점과 4개의 삼각형 2차원 와이어 프레임 도형렌더링
	static constexpr float squareHalfSize = 0.5f;
	static constexpr size_t vertexCount = 5;
	static constexpr size_t triangleCount = 4;

	// 메시를 구성하는 정점 배열
	static constexpr std::array<Vertex2D, vertexCount> rawVertices =
	{
		//	-0.5, -0.5,	/	Red
		//	-0.5, 0.5	/	Green
		//	0.5, 0.5	/	Blue
		//	0.5, -0.5	/	White
		//	0, 0		/	Black
		Vertex2D(Vector2(-squareHalfSize, -squareHalfSize), LinearColor(1.f, 0.f, 0.f)), 	
		Vertex2D(Vector2(-squareHalfSize, squareHalfSize), LinearColor(0.f, 1.f, 0.f)),		
		Vertex2D(Vector2(squareHalfSize, squareHalfSize), LinearColor(0.f, 0.f, 1.f)),		
		Vertex2D(Vector2(squareHalfSize, -squareHalfSize), LinearColor(1.f, 1.f, 1.f)),		
		Vertex2D(Vector2(0, 0), LinearColor(0.f, 0.f, 0.f)),								
	};

	// 메시를 구성하는 인덱스 배열
	static constexpr std::array<size_t, triangleCount * 3> indices =
	{
		0, 1, 4,
		1, 2, 4,
		2, 3, 4,
		0, 3, 4
	};
	// 행렬을 적용한 메시 정보를 사용해 물체를 렌더링
	static std::vector<Vertex2D> vertices(vertexCount);
	for (size_t vi = 0; vi < vertexCount; ++vi)
	{
		vertices[vi].Position = finalMatrix * rawVertices[vi].Position;
		vertices[vi].Color = rawVertices[vi].Color;
	}

	// 변환된 정점을 잇는 선 그리기
	for (size_t ti = 0; ti < triangleCount; ++ti)
	{
		size_t bi = ti * 3;
		
		/// 예제 8_2-8_1영역 색칠하기 
		std::array<Vertex2D, 3> tv = {
			vertices[indices[bi]], vertices[indices[bi + 1]], vertices[indices[bi + 2]]};

		Vector2 minPos(Math::Min3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
			Math::Min3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));
		Vector2 maxPos(Math::Max3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
			Math::Max3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));

		// 무게 중심좌표를 위한 준비작업
		Vector2 u = tv[1].Position - tv[0].Position;
		Vector2 v = tv[2].Position - tv[0].Position;

		// 공통 분모 ( uu * vv - uv * uv )
		float udotv = u.Dot(v);
		float vdotv = v.Dot(v);
		float udotu = u.Dot(u);
		float denominator = udotv * udotv - vdotv * udotu;

		// 퇴화삼각형은 그리지 않음
		if (denominator == 0.0f)
		{
			continue;
		}

		float invDenominator = 1.f / denominator;
		// 화면상의 점 구하기
		ScreenPoint lowerLeftPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, minPos);
		ScreenPoint upperRightPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, maxPos);

		// 두 점이 화면 밖을 벗어나는 경우 클리핑 처리
		lowerLeftPoint.X = Math::Max(0, lowerLeftPoint.X);
		lowerLeftPoint.Y = Math::Min(_ScreenSize.Y, lowerLeftPoint.Y);
		upperRightPoint.X = Math::Min(_ScreenSize.X, upperRightPoint.X);
		upperRightPoint.Y = Math::Max(0, upperRightPoint.Y);

		// 삼각형을 둘러싼 사각형 영역의 픽셀을 모두 순회
		for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
		{
			for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
			{
				ScreenPoint fragment = ScreenPoint(x, y);
				Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
				Vector2 w = pointToTest - tv[0].Position;
				float wdotu = w.Dot(u);
				float wdotv = w.Dot(v);

				// 분자 값을 구하고 최종 무게중심좌표 산출
				float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
				float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
				float oneMinusST = 1.f - s - t;

				// 컨벡스 조건을 만족할 때만 점 찍기
				if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
				{
					LinearColor outColor = tv[0].Color * oneMinusST + tv[1].Color * s + tv[2].Color * t;
					r.DrawPoint(fragment, outColor);
				}
			}
		}

		r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 1]].Position, LinearColor::Black);
		r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 2]].Position, LinearColor::Black);
		r.DrawLine(vertices[indices[bi + 1]].Position, vertices[indices[bi + 2]].Position, LinearColor::Black);
	}
}

// 메시를 그리는 함수
void SoftRenderer::DrawMesh2D(const class DD::Mesh& InMesh, const Matrix3x3& InMatrix, const LinearColor& InColor)
{
}

// 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle2D(std::vector<DD::Vertex2D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
}

텍스처 매핑

위 예제 처럼 메시에 이미지를 입히기 위해 변환된 데이터를 텍스처라고 부른다.

그리고 이런 색상 데이터를 메시에 입히는 작업을 텍스처 매핑이라고 부른다.

텍스처는 관리 방식을 통일하기 위해 원본의 해상도와 관계 없이 가로 세로 크기를 1로 정규화하여 사용한다. 그렇기 때문에 텍스처를 사용할 때에는 항상 0부터 1 사이의 값으로 정규화된 2차원 좌표계를 사용하며, 가로 정보는 U, 세로 정보는 V로 지정하여 2차원 벡터를 사용한다.

이것을 UV좌표계라 부른다.

예제 8_4 텍스처 매핑하기

이전 예제들과 비교하기 위해 조금 비효율 적이더라고 텍스처 매핑상자를 1초 주기로 이전 예제에 덮어씌워 렌더링 하도록 하겟다.

타이머용 시간 변수 CurrentTime

// 게임 로직과 렌더링 로직이 공유하는 변수
float currentTime = 0.f;

Update2D함수

	currentTime += InDeltaSeconds;

Render2D함수

	const auto& texture = g.GetTexture(GameEngine::BaseTexture);

if (currentTime > 1.f)
{
	if (currentTime > 2.f)
	{
		currentTime = 0.f;
	}
	// 텍스처 매핑용 변수
	static constexpr size_t vertexCount_2 = 4;
	static constexpr size_t triangleCount_2 = 2;

	// 텍스처 매핑용 정점 배열
	static constexpr std::array<Vertex2D, vertexCount_2> rawVertices_2 =
	{
		Vertex2D(Vector2(-squareHalfSize, -squareHalfSize), LinearColor(), Vector2(0.125f, 0.75f)),
		Vertex2D(Vector2(-squareHalfSize, squareHalfSize), LinearColor(), Vector2(0.125f, 0.875f)),
		Vertex2D(Vector2(squareHalfSize, squareHalfSize), LinearColor(), Vector2(0.25f, 0.875f)),
		Vertex2D(Vector2(squareHalfSize, -squareHalfSize), LinearColor(), Vector2(0.25f, 0.75f)),
	};
	// 텍스처 매핑용 인덱스 배열
	static constexpr std::array<size_t, triangleCount_2 * 3> indices_2 =
	{
		0, 1, 2,
		0, 2, 3,
	};
	// 텍스처 매핑용 렌더링
	static std::vector<Vertex2D> vertices_2(vertexCount_2);
	for (size_t vi = 0; vi < vertexCount_2; ++vi)
	{
		vertices_2[vi].Position = finalMatrix * rawVertices_2[vi].Position;
		vertices_2[vi].UV = rawVertices_2[vi].UV;
	}
	// 변환된 정점을 잇는 선 그리기
	for (size_t ti = 0; ti < triangleCount_2; ++ti)
	{
		size_t bi = ti * 3;

		/// 예제 8_2-8_1영역 색칠하기 
		std::array<Vertex2D, 3> tv = {
			vertices_2[indices_2[bi]], vertices_2[indices_2[bi + 1]], vertices_2[indices_2[bi + 2]] };

		Vector2 minPos(Math::Min3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
			Math::Min3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));
		Vector2 maxPos(Math::Max3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
			Math::Max3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));

		// 무게 중심좌표를 위한 준비작업
		Vector2 u = tv[1].Position - tv[0].Position;
		Vector2 v = tv[2].Position - tv[0].Position;

		// 공통 분모 ( uu * vv - uv * uv )
		float udotv = u.Dot(v);
		float vdotv = v.Dot(v);
		float udotu = u.Dot(u);
		float denominator = udotv * udotv - vdotv * udotu;

		// 퇴화삼각형은 그리지 않음
		if (denominator == 0.0f)
		{
			continue;
		}

		float invDenominator = 1.f / denominator;
		// 화면상의 점 구하기
		ScreenPoint lowerLeftPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, minPos);
		ScreenPoint upperRightPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, maxPos);

		// 두 점이 화면 밖을 벗어나는 경우 클리핑 처리
		lowerLeftPoint.X = Math::Max(0, lowerLeftPoint.X);
		lowerLeftPoint.Y = Math::Min(_ScreenSize.Y, lowerLeftPoint.Y);
		upperRightPoint.X = Math::Min(_ScreenSize.X, upperRightPoint.X);
		upperRightPoint.Y = Math::Max(0, upperRightPoint.Y);

		// 삼각형을 둘러싼 사각형 영역의 픽셀을 모두 순회
		for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
		{
			for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
			{
				ScreenPoint fragment = ScreenPoint(x, y);
				Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
				Vector2 w = pointToTest - tv[0].Position;
				float wdotu = w.Dot(u);
				float wdotv = w.Dot(v);

				// 분자 값을 구하고 최종 무게중심좌표 산출
				float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
				float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
				float oneMinusST = 1.f - s - t;

				// 컨벡스 조건을 만족할 때만 점 찍기
				if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
				{
					Vector2 targetUV = tv[0].UV * oneMinusST + tv[1].UV * s + tv[2].UV * t;
					r.DrawPoint(fragment, texture.GetSample(targetUV));
				}
			}
		}
	}
}

전체 코드는 다음과 같습니다.

#include "Precompiled.h"
#include "SoftRenderer.h"
#include <random>
using namespace CK::DD;

// 격자를 그리는 함수
void SoftRenderer::DrawGizmo2D()
{
	auto& r = GetRenderer();
	const auto& g = Get2DGameEngine();

	// 그리드 색상
	LinearColor gridColor(LinearColor(0.8f, 0.8f, 0.8f, 0.3f));

	// 뷰의 영역 계산
	Vector2 viewPos = g.GetMainCamera().GetTransform().GetPosition();
	Vector2 extent = Vector2(_ScreenSize.X * 0.5f, _ScreenSize.Y * 0.5f);

	// 좌측 하단에서부터 격자 그리기
	int xGridCount = _ScreenSize.X / _Grid2DUnit;
	int yGridCount = _ScreenSize.Y / _Grid2DUnit;

	// 그리드가 시작되는 좌하단 좌표 값 계산
	Vector2 minPos = viewPos - extent;
	Vector2 minGridPos = Vector2(ceilf(minPos.X / (float)_Grid2DUnit), ceilf(minPos.Y / (float)_Grid2DUnit)) * (float)_Grid2DUnit;
	ScreenPoint gridBottomLeft = ScreenPoint::ToScreenCoordinate(_ScreenSize, minGridPos - viewPos);

	for (int ix = 0; ix < xGridCount; ++ix)
	{
		r.DrawFullVerticalLine(gridBottomLeft.X + ix * _Grid2DUnit, gridColor);
	}

	for (int iy = 0; iy < yGridCount; ++iy)
	{
		r.DrawFullHorizontalLine(gridBottomLeft.Y - iy * _Grid2DUnit, gridColor);
	}

	ScreenPoint worldOrigin = ScreenPoint::ToScreenCoordinate(_ScreenSize, -viewPos);
	r.DrawFullHorizontalLine(worldOrigin.Y, LinearColor::Red);
	r.DrawFullVerticalLine(worldOrigin.X, LinearColor::Green);

}

// 게임 오브젝트 목록


// 최초 씬 로딩을 담당하는 함수
void SoftRenderer::LoadScene2D()
{
	// 최초 씬 로딩에서 사용하는 모듈 내 주요 레퍼런스
	auto& g = Get2DGameEngine();

}

// 게임 로직과 렌더링 로직이 공유하는 변수
Vector2 currentPosition;
float currentScale = 100.f;
float currentDegree = 0.f;
float currentTime = 0.f;
// 게임 로직을 담당하는 함수
void SoftRenderer::Update2D(float InDeltaSeconds)
{
	currentTime += InDeltaSeconds;

	// 게임 로직에서 사용하는 모듈 내 주요 레퍼런스
	auto& g = Get2DGameEngine();
	const InputManager& input = g.GetInputManager();

	// 게임 로직의 로컬 변수
	static float moveSpeed = 100.f;
	static float scaleMin = 50.f;
	static float scaleMax = 200.f;
	static float scaleSpeed = 100.f;
	static float rotateSpeed = 180.f;

	Vector2 inputVector = Vector2(input.GetAxis(InputAxis::XAxis), input.GetAxis(InputAxis::YAxis)).GetNormalize();
	Vector2 deltaPosition = inputVector * moveSpeed * InDeltaSeconds;
	float deltaScale = input.GetAxis(InputAxis::ZAxis) * scaleSpeed * InDeltaSeconds;
	float deltaDegree = input.GetAxis(InputAxis::WAxis) * rotateSpeed * InDeltaSeconds;

	// 물체의 최종 상태 설정
	currentPosition += deltaPosition;
	currentScale = Math::Clamp(currentScale + deltaScale, scaleMin, scaleMax);
	currentDegree += deltaDegree;
}

// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render2D()
{
	// 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
	auto& r = GetRenderer();
	const auto& g = Get2DGameEngine();

	const auto& texture = g.GetTexture(GameEngine::BaseTexture);


	// 배경에 격자 그리기
	DrawGizmo2D();

	// 메시 데이터의 선언


	// 아핀 변환 행렬 ( 크기 ) 
	Vector3 sBasis1(currentScale, 0.f, 0.f);
	Vector3 sBasis2(0.f, currentScale, 0.f);
	Vector3 sBasis3 = Vector3::UnitZ;
	Matrix3x3 sMatrix(sBasis1, sBasis2, sBasis3);

	// 아핀 변환 행렬 ( 회전 ) 
	float sin = 0.f, cos = 0.f;
	Math::GetSinCos(sin, cos, currentDegree);
	Vector3 rBasis1(cos, sin, 0.f);
	Vector3 rBasis2(-sin, cos, 0.f);
	Vector3 rBasis3 = Vector3::UnitZ;
	Matrix3x3 rMatrix(rBasis1, rBasis2, rBasis3);

	// 아핀 변환 행렬 ( 이동 ) 
	Vector3 tBasis1 = Vector3::UnitX;
	Vector3 tBasis2 = Vector3::UnitY;
	Vector3 tBasis3(currentPosition.X, currentPosition.Y, 1.f);
	Matrix3x3 tMatrix(tBasis1, tBasis2, tBasis3);

	// 모든 아핀 변환을 곱한 합성 행렬. 크기-회전-이동 순으로 적용
	Matrix3x3 finalMatrix = tMatrix * rMatrix * sMatrix;

	// 현재 위치, 크기, 각도를 화면에 출력
	r.PushStatisticText(std::string("Position : ") + currentPosition.ToString());
	r.PushStatisticText(std::string("Scale : ") + std::to_string(currentScale));
	r.PushStatisticText(std::string("Degree : ") + std::to_string(currentDegree));
	
	/// 예제 8_1 5개의 정점과 4개의 삼각형 2차원 와이어 프레임 도형렌더링
	static constexpr float squareHalfSize = 0.5f;
	static constexpr size_t vertexCount = 5;
	static constexpr size_t triangleCount = 4;

	// 메시를 구성하는 정점 배열
	static constexpr std::array<Vertex2D, vertexCount> rawVertices =
	{
		//	-0.5, -0.5,	/	Red
		//	-0.5, 0.5	/	Green
		//	0.5, 0.5	/	Blue
		//	0.5, -0.5	/	White
		//	0, 0		/	Black
		Vertex2D(Vector2(-squareHalfSize, -squareHalfSize), LinearColor(1.f, 0.f, 0.f)),
		Vertex2D(Vector2(-squareHalfSize, squareHalfSize), LinearColor(0.f, 1.f, 0.f)),
		Vertex2D(Vector2(squareHalfSize, squareHalfSize), LinearColor(0.f, 0.f, 1.f)),
		Vertex2D(Vector2(squareHalfSize, -squareHalfSize), LinearColor(1.f, 1.f, 1.f)),
		Vertex2D(Vector2(0, 0), LinearColor(0.f, 0.f, 0.f)),
	};
	// 메시를 구성하는 인덱스 배열
	static constexpr std::array<size_t, triangleCount * 3> indices =
	{
		0, 1, 4,
		1, 2, 4,
		2, 3, 4,
		0, 3, 4
	};

	// 행렬을 적용한 메시 정보를 사용해 물체를 렌더링
	static std::vector<Vertex2D> vertices(vertexCount);
	for (size_t vi = 0; vi < vertexCount; ++vi)
	{
		vertices[vi].Position = finalMatrix * rawVertices[vi].Position;
		vertices[vi].Color = rawVertices[vi].Color;
	}

	// 변환된 정점을 잇는 선 그리기
	for (size_t ti = 0; ti < triangleCount; ++ti)
	{
		size_t bi = ti * 3;
		
		/// 예제 8_2-8_1영역 색칠하기 
		std::array<Vertex2D, 3> tv = {
			vertices[indices[bi]], vertices[indices[bi + 1]], vertices[indices[bi + 2]]};

		Vector2 minPos(Math::Min3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
			Math::Min3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));
		Vector2 maxPos(Math::Max3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
			Math::Max3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));

		// 무게 중심좌표를 위한 준비작업
		Vector2 u = tv[1].Position - tv[0].Position;
		Vector2 v = tv[2].Position - tv[0].Position;

		// 공통 분모 ( uu * vv - uv * uv )
		float udotv = u.Dot(v);
		float vdotv = v.Dot(v);
		float udotu = u.Dot(u);
		float denominator = udotv * udotv - vdotv * udotu;

		// 퇴화삼각형은 그리지 않음
		if (denominator == 0.0f)
		{
			continue;
		}

		float invDenominator = 1.f / denominator;
		// 화면상의 점 구하기
		ScreenPoint lowerLeftPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, minPos);
		ScreenPoint upperRightPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, maxPos);

		// 두 점이 화면 밖을 벗어나는 경우 클리핑 처리
		lowerLeftPoint.X = Math::Max(0, lowerLeftPoint.X);
		lowerLeftPoint.Y = Math::Min(_ScreenSize.Y, lowerLeftPoint.Y);
		upperRightPoint.X = Math::Min(_ScreenSize.X, upperRightPoint.X);
		upperRightPoint.Y = Math::Max(0, upperRightPoint.Y);

		// 삼각형을 둘러싼 사각형 영역의 픽셀을 모두 순회
		for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
		{
			for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
			{
				ScreenPoint fragment = ScreenPoint(x, y);
				Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
				Vector2 w = pointToTest - tv[0].Position;
				float wdotu = w.Dot(u);
				float wdotv = w.Dot(v);

				// 분자 값을 구하고 최종 무게중심좌표 산출
				float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
				float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
				float oneMinusST = 1.f - s - t;

				// 컨벡스 조건을 만족할 때만 점 찍기
				if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
				{
					LinearColor outColor = tv[0].Color * oneMinusST + tv[1].Color * s + tv[2].Color * t;
					r.DrawPoint(fragment, outColor);
				}
			}
		}

		r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 1]].Position, LinearColor::Black);
		r.DrawLine(vertices[indices[bi]].Position, vertices[indices[bi + 2]].Position, LinearColor::Black);
		r.DrawLine(vertices[indices[bi + 1]].Position, vertices[indices[bi + 2]].Position, LinearColor::Black);
	}
	if (currentTime > 1.f)
	{
		if (currentTime > 2.f)
		{
			currentTime = 0.f;
		}
		// 텍스처 매핑용 변수
		static constexpr size_t vertexCount_2 = 4;
		static constexpr size_t triangleCount_2 = 2;

		// 텍스처 매핑용 정점 배열
		static constexpr std::array<Vertex2D, vertexCount_2> rawVertices_2 =
		{
			Vertex2D(Vector2(-squareHalfSize, -squareHalfSize), LinearColor(), Vector2(0.125f, 0.75f)),
			Vertex2D(Vector2(-squareHalfSize, squareHalfSize), LinearColor(), Vector2(0.125f, 0.875f)),
			Vertex2D(Vector2(squareHalfSize, squareHalfSize), LinearColor(), Vector2(0.25f, 0.875f)),
			Vertex2D(Vector2(squareHalfSize, -squareHalfSize), LinearColor(), Vector2(0.25f, 0.75f)),
		};
		// 텍스처 매핑용 인덱스 배열
		static constexpr std::array<size_t, triangleCount_2 * 3> indices_2 =
		{
			0, 1, 2,
			0, 2, 3,
		};
		// 텍스처 매핑용 렌더링
		static std::vector<Vertex2D> vertices_2(vertexCount_2);
		for (size_t vi = 0; vi < vertexCount_2; ++vi)
		{
			vertices_2[vi].Position = finalMatrix * rawVertices_2[vi].Position;
			vertices_2[vi].UV = rawVertices_2[vi].UV;
		}
		// 변환된 정점을 잇는 선 그리기
		for (size_t ti = 0; ti < triangleCount_2; ++ti)
		{
			size_t bi = ti * 3;

			/// 예제 8_2-8_1영역 색칠하기 
			std::array<Vertex2D, 3> tv = {
				vertices_2[indices_2[bi]], vertices_2[indices_2[bi + 1]], vertices_2[indices_2[bi + 2]] };

			Vector2 minPos(Math::Min3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
				Math::Min3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));
			Vector2 maxPos(Math::Max3(tv[0].Position.X, tv[1].Position.X, tv[2].Position.X),
				Math::Max3(tv[0].Position.Y, tv[1].Position.Y, tv[2].Position.Y));

			// 무게 중심좌표를 위한 준비작업
			Vector2 u = tv[1].Position - tv[0].Position;
			Vector2 v = tv[2].Position - tv[0].Position;

			// 공통 분모 ( uu * vv - uv * uv )
			float udotv = u.Dot(v);
			float vdotv = v.Dot(v);
			float udotu = u.Dot(u);
			float denominator = udotv * udotv - vdotv * udotu;

			// 퇴화삼각형은 그리지 않음
			if (denominator == 0.0f)
			{
				continue;
			}

			float invDenominator = 1.f / denominator;
			// 화면상의 점 구하기
			ScreenPoint lowerLeftPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, minPos);
			ScreenPoint upperRightPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, maxPos);

			// 두 점이 화면 밖을 벗어나는 경우 클리핑 처리
			lowerLeftPoint.X = Math::Max(0, lowerLeftPoint.X);
			lowerLeftPoint.Y = Math::Min(_ScreenSize.Y, lowerLeftPoint.Y);
			upperRightPoint.X = Math::Min(_ScreenSize.X, upperRightPoint.X);
			upperRightPoint.Y = Math::Max(0, upperRightPoint.Y);

			// 삼각형을 둘러싼 사각형 영역의 픽셀을 모두 순회
			for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
			{
				for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
				{
					ScreenPoint fragment = ScreenPoint(x, y);
					Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
					Vector2 w = pointToTest - tv[0].Position;
					float wdotu = w.Dot(u);
					float wdotv = w.Dot(v);

					// 분자 값을 구하고 최종 무게중심좌표 산출
					float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
					float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
					float oneMinusST = 1.f - s - t;

					// 컨벡스 조건을 만족할 때만 점 찍기
					if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
					{
						Vector2 targetUV = tv[0].UV * oneMinusST + tv[1].UV * s + tv[2].UV * t;
						r.DrawPoint(fragment, texture.GetSample(targetUV));
					}
				}
			}
		}
	}
}

// 메시를 그리는 함수
void SoftRenderer::DrawMesh2D(const class DD::Mesh& InMesh, const Matrix3x3& InMatrix, const LinearColor& InColor)
{
}

// 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle2D(std::vector<DD::Vertex2D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
}

이번 8장을 학습하면서 어리숙하게 알고 있던 UV 매핑과 텍스쳐, 그리고 버텍스에 대해서 정확하게 알게 되어 기쁘다.

이 다음장 부터는 3D프로젝트를 진행하게 된다. 또 무엇을 배울지 기대된다.

모든 예제 코드의 소스파일은

GitHub - onlybooks/gamemath: <이득우의 게임 수학> 공식 깃허브 페이지

<이득우의 게임 수학> 공식 깃허브 페이지. Contribute to onlybooks/gamemath development by creating an account on GitHub.

github.com

또한 제 개인 깃허브 레포지토리 에 있습니다.

Workspace/C++/GameMath at main · cyphen156/Workspace · GitHub

Workspace/C++/GameMath at main · cyphen156/Workspace

Studying . Contribute to cyphen156/Workspace development by creating an account on GitHub.

github.com

※ 이득우 교수님의 인프런 게임수학강의를 참고하여 작성되었습니다.

컨벡스 영역 내의 두 점을 연결한 선분을 만들었을 때 그 선분은 항상 영역 안에 속한다. [본문으로]

저작자표시

'수학 > 게임수학' 카테고리의 다른 글

게임 수학 10장 : 3차원 공간(입체 공간의 생성)-3차원 트랜스폼과 오일러각 (1)	2025.03.24
게임 수학 9장 : 게임 엔진(콘텐츠를 만드는 기술) (3)	2025.03.21
게임 수학 7장-2 : 내적(벡터 공간의 분석과 응용)-조명과 투영 (0)	2025.03.17
게임 수학 7장-1 : 내적(벡터 공간의 분석과 응용)-벡터 내적과 시야 (0)	2025.03.13
게임 수학 6장 : 아핀공간: 움직이는 가상 세계의 구축 (0)	2025.03.12

'수학/게임수학' Related Articles

cyphen156 Cyphen의 개인 공부 블로그입니다. 프사는 아는 동생이 그려준 그림 주인장과 싱크로율 0%

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

cyphen156

cyphen156

게임 수학 8장 : 삼각형(물체를 구성하는 가장 작은 단위)-메시와 텍스쳐 본문

게임 수학 8장 : 삼각형(물체를 구성하는 가장 작은 단위)-메시와 텍스쳐

정점(Vertex), 삼각형(Triangle), 폴리곤(Polygon)

정점(Vertex)과 메시(Mesh)

정점버퍼와 인덱스 버퍼

와이어 프레임

예제 8_1 5개의 정점과 4개의 삼각형 2차원 와이어 프레임 도형렌더링

무게 중심 좌표

예제 8_2-8_1영역색칠하기

예제 8_3 사각형 버텍스 정보로 색칠하기

예제 8_3의 최종 코드는 다음과 같다.

텍스처 매핑

예제 8_4 텍스처 매핑하기

'수학 > 게임수학' 카테고리의 다른 글

티스토리툴바

개인정보

단축키

내 블로그

블로그 게시글

모든 영역