선형대수학 #0 The Geometry of Linear Equations

스트랭 교수는 1강에 선형방정식의 기하학적 의미에 대해 설명해준다. 

예를 들어 두 개의 미지수와 두 개의 방정식이 존재하는 경우에 대해 생각해보자.

2x-y=0, -x + 2y = 3

이 방정식들을 행렬을 통해 표현하면 

A(행렬)X(벡터) = b(벡터)라는 결과가 도출된다.

행의 선형 조합(Linear Combinations of rows Picture)

위의 두 방정식을 행을 기준으로 풀이하면 다음과 같다. 두 직선의 교점을 구해 유일한 해를 구하게 된다.

그런데 이 문제를 푸는 방법은 하나가 아니다.

열의 선형 조합(Linear Combinations of calumns Picture)

이것을 다른 방법인 열을 기준으로 풀이해 보면 다음과 같이 표현된다.

두 벡터(2, -1)과 (-1, 2)를 조합하여 (0, 3)이라는 새로운 벡터를 만들어 내야 하는 것이다.

그 해답은 다음과 같은 그림으로 볼 수 있다.

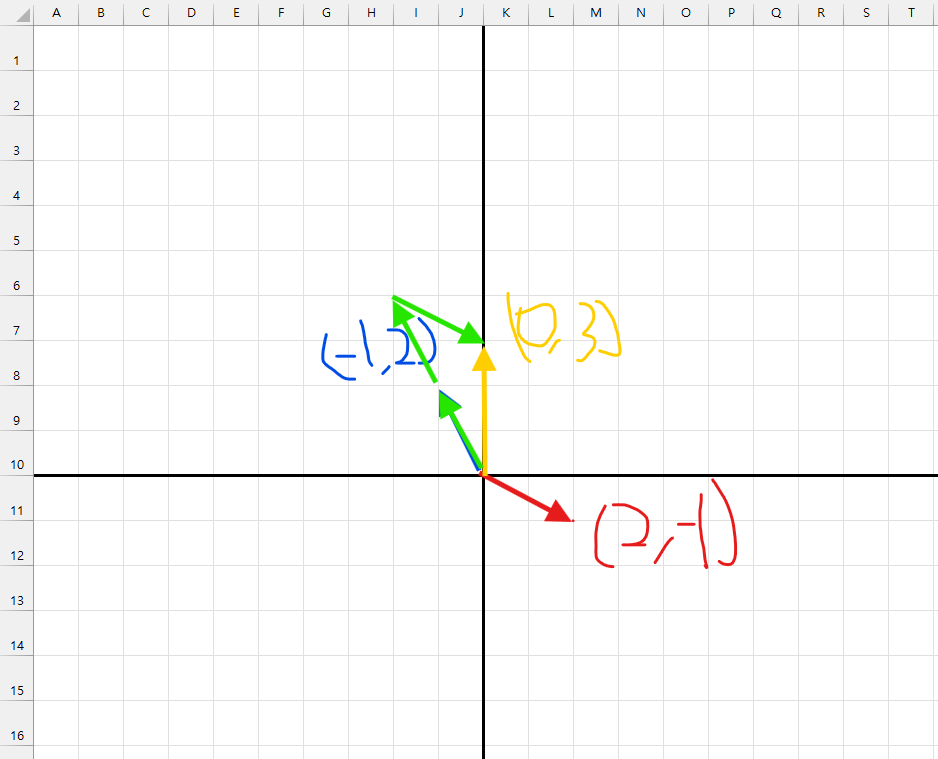
1스칼라 * X벡터 + 2스칼라 * Y벡터 = b벡터의 결과가 도출된다. 이것은 벡터의 기본 원칙중 하나, 선형 독립성을 만족하기 때문에 가능한 것이다. 

두 벡터가 선형 의존관계(같은 기울기)에 존재하지 않기 때문에 이 둘을 조합하여 어떠한 벡터든 만들어 낼 수 있기 때문이다.

이 선형 독립성은 굉장히 중요하다. 조금 더 응용해보자면 세 벡터를 통한 벡터 생성의 경우 순차적으로 A, B, C라는 벡터를 선형 조합을 통해 생성하게 되는데, 두 벡터가 선형 독립이라면 어떠한 벡터든 만들어낼 수 있으므로 그 다음벡터와의 선형 조합 또한 항상 생성가능하기 때문에 해가 무수히 많아진다(유일한 해를 찾을 수 없다). 

이것에 대한 예시는 다음과 같다. 

세개의 미지수와 세개의 방정식이 있다고 생각하자.

이번엔 단번에 행렬로 표시해보면 다음과 같다.

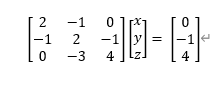
미지수가 3개 이기 때문에 좌표 평면의 차원이 2차원이 아닌 3차원으로 확장되어 표현된다. 

투명도가 적용된 줄들은 그만큼 X와 Y축의 좌표가 평행이동하여 2차원 좌표평면 자체가 움직인 상태라고 이해해주면 감사하겠습니다.

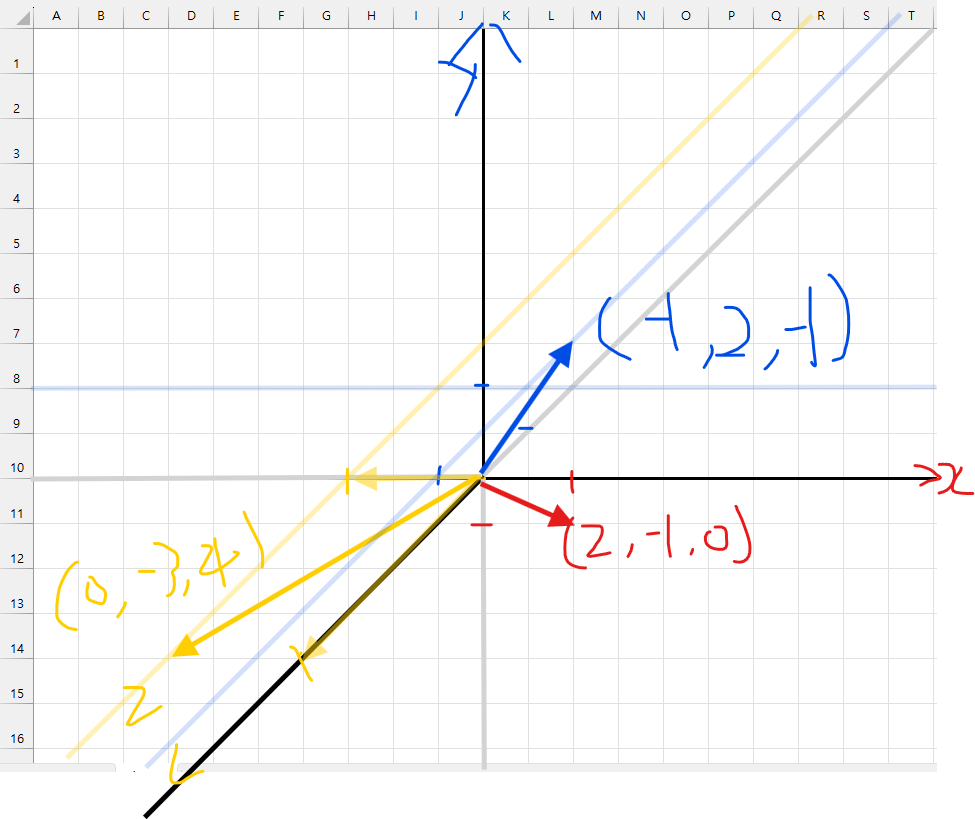
어떠한가? 딱봐도 3차원 공간을 그리는것이 난잡해지지 않았는가? 이제 이 벡터들을 조합하여 (0, -1, 4)로 향하는 벡터를 생성하면 된다. 

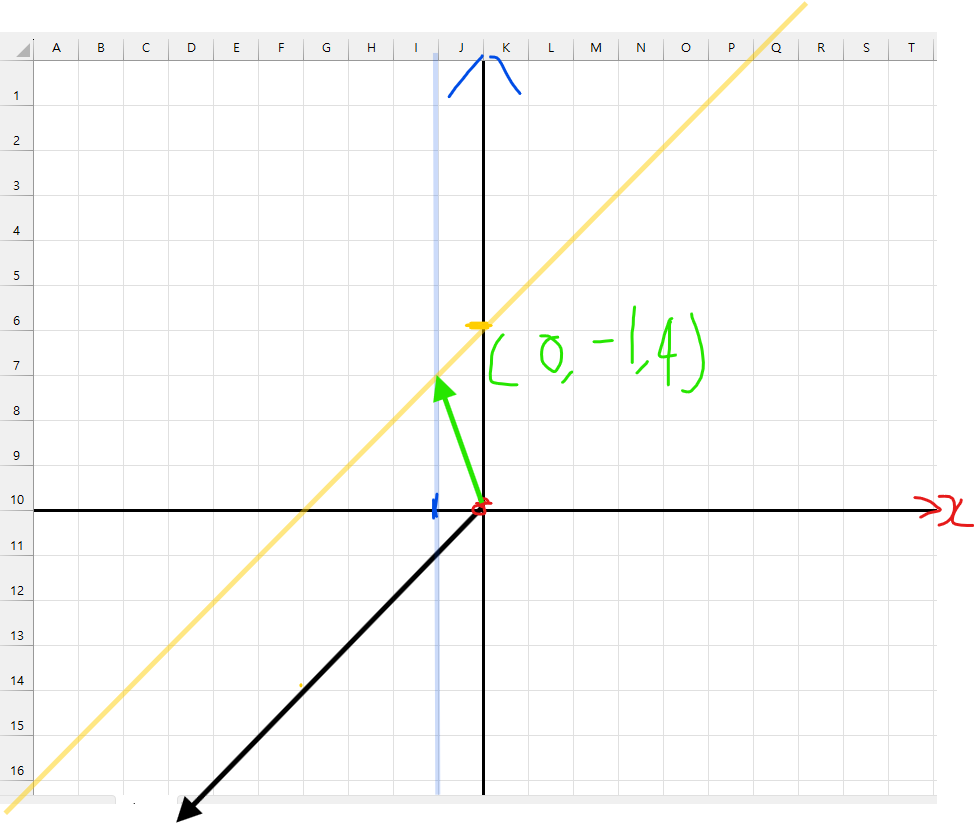
여기서 핵심은 한 평면 위에서는 정답을 표현할 수 없다는 것이다.

조금 더 명확하게 게임 엔진을 사용해서 표현해 보겠다. 

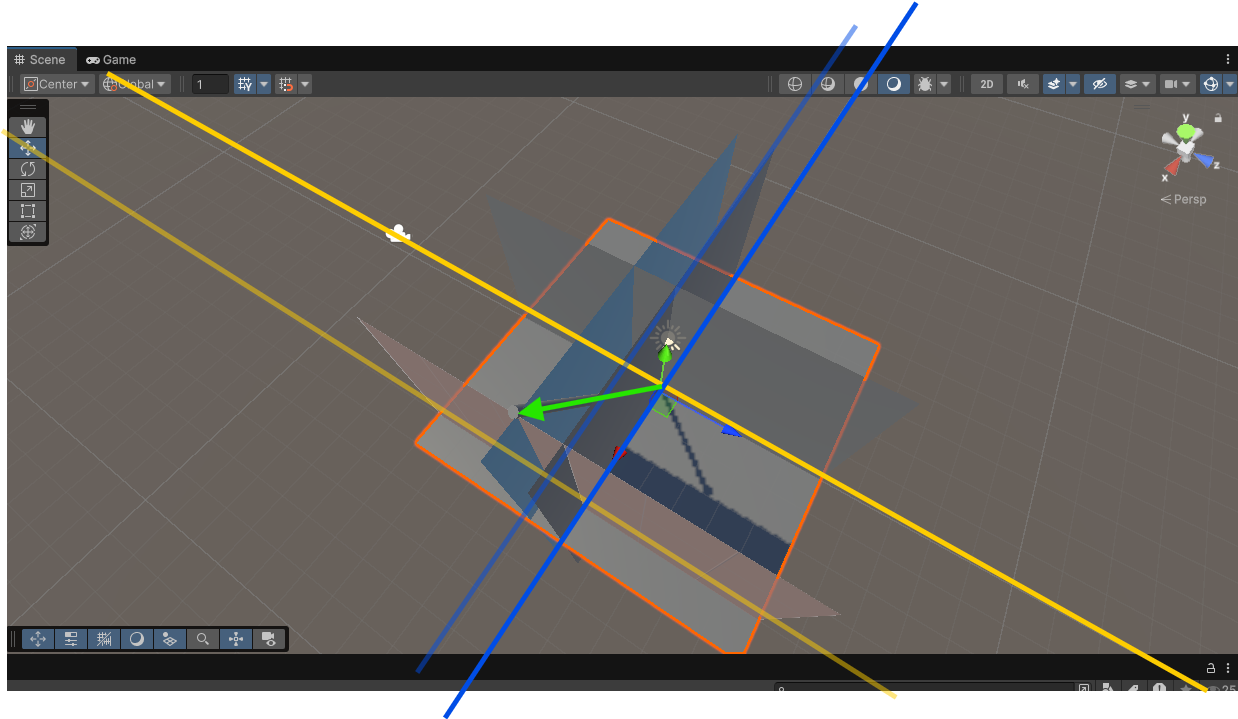
좌표가 조금 뒤틀리긴 했지만 어쨋든 막대 기둥을 통해 표현되기는 한다.

여기서 시사하는 바는 세 벡터가 선형 독립이기 때문에 어떻게든 답을 구할 수 있다는 것이다. 

반대로 말해 선형 의존인 상태 즉, 세 벡터 중 어느 하나가 우연히도 다른 벡터와 같은 평면 위에 존재한다면, 다른 평면으로 향하는 벡터를 절대 구할 수 없다는 것을 의미한다. 현실로 치면 앞으로 가거나 뒤로 가는 방향만 존재(1차원)하고 옆(2차원으로의 확장)으로 간다는 선택지가 사라진다는 것이다. 
또는 좌표평면의 360도 방향(2차원 공간/좌표 평면)으로 움직일 수 있지만, 위로 가거나 아래(3차원 공간)로 내려가는 행위를 할 수 없게 된다는 것을 의미한다. 

게임 수학때 잠깐 배웟던 것을 상기하면 역시 벡터공간을 상상하기란 참 어렵지 싶다. 

결국 N차원에 N개의 벡터가 존재할 때 어떤 한 벡터를 향하는 해를 구하고 싶다면 모든 벡터가 선형 독립이어야 한다는 결론이 나온다.