cyphen156
아핀공간과 삼각함수의 항등법칙에 대한 궁금증 본문
아핀공간에서는 한 차원에서 점의 이동을 구현하기 위해 한단계 상위 차원을 이용한다.
가령 1차원인 점과 선분의 이동을 표현하기 위해서 2차원 좌표계를 사용하고, 2차원에서의 평면도형의 이동을 구현하기 위해서 삼차원 공간을 사용한다. 그리고 3차원 공간에서 입방체의 이동과 회전을 구현하기 위해 4차원인 쿼터니언을 사용한다.
이렇게 상위차원을 이용하는 이유는 벡터의 변환은 늘이거나 줄이거나 할 수는 있지만 항상 원점에 접해야 한다는 대원칙이 존재하기 때문이다. 그렇기 때문에 같은 차원내에서는 항상 원점에서 벗어날 수 없기 때문에 물체의 좌표 자체가 이동할 수 없는 것이다. 그런데 상위 차원을 이용한다면 우리가 눈으로 확인할 수는 없지만 개념적으로 원점에 해당하는 한 좌표가 존재한다고 가정하고 물체의 이동을 구현할 수 있게 된다.
여기서 알 수 있는 점은 마지막 차원, 즉 상위차원은 좌표계 상에서 항상 같은 위치를 표현하게 된다. 상위차원의 원점에 해당하는 0에 위치해 있다는 것을 의미한다.
그리고 이동하는 물체의 상위차원상의 좌표계는 항상 1이 되어야 한다. 그렇기 때문에 두 점의 선형 결합을 수식적으로 표현하면 다음과 같이 표현되는데
aP1(x1, y1, 1) + bP2(x2, y2, 1) = P3(ax1 + bx2, ay1 + by2, 1)
여기서 도출할 수 있는 것은 a + b = 1이 성립한다는 사실이다.
이것을 아핀결합이라고 표현하며 아핀 결합에 의해 두 점의 결합은 선형성을 띄고, 선형 의존관계에 속하게 된다. 그렇기때문에 직선위의 어떠한 좌표든 새로 생성할 수 있게 한다. 여기서 말하는 직선은 같은 차원 내에서 라는 말로 다시 변환된다.
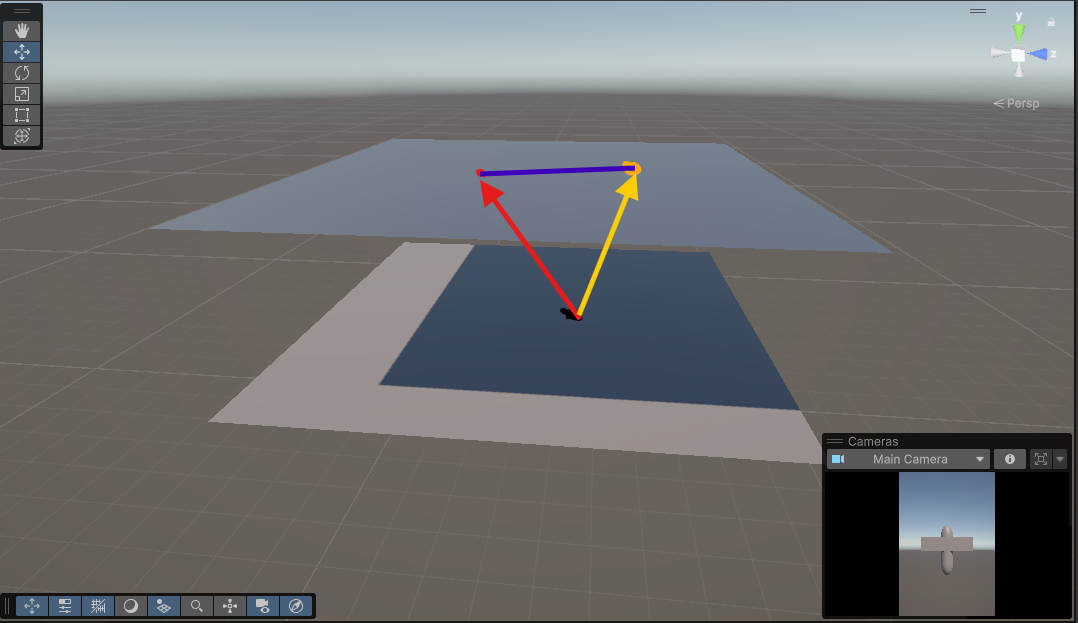
삼각 함수에도 똑같은 것이 있다. Sin**2 + Cos**2 = 1 이라는 항등식이다.
위 항등식은 피타고라스의 정리에 의해 빗변(R) = x**2 + y**2을 R = 1로 정규화 한 항등원 내에서 성립하는 수식이다.
그렇다면 위 그림에서 검은 점을 원점이라고 본다면 빨간 점을 향하는 벡터또한 1, 노란 점을 향하는 벡터 또한 1이라는 일반화 관계가 성립함을 볼 수 있고각 좌표계는 sin**2 + cos**2 = 1로 향하는 빨간 점의 x1, y1좌표를, 노란 점으로 향하는 x1, y1좌표를 구할 수 있음을 볼 수 있다.
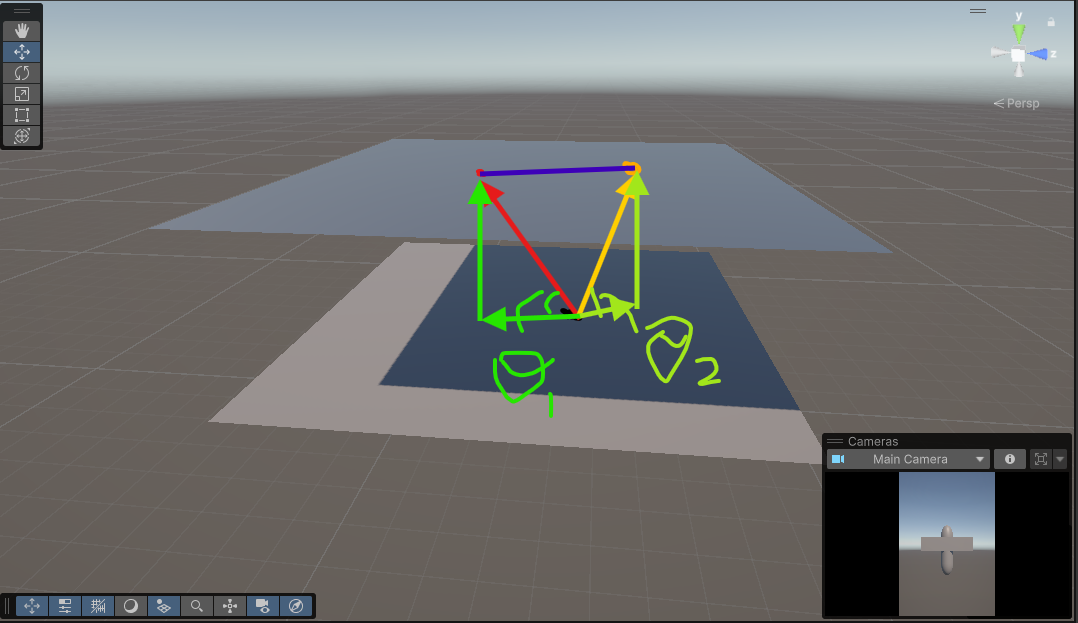
주저리 주저리 어지럽게 보여주고 있는데 결론은 다음과 같다.
아핀 결합은 삼각함수와 연관이 있다는 것이다.
'수학 > 게임수학' 카테고리의 다른 글
| 게임 수학 7장-1 : 내적(벡터 공간의 분석과 응용)-벡터 내적과 시야 (0) | 2025.03.13 |
|---|---|
| 게임 수학 6장 : 아핀공간: 움직이는 가상 세계의 구축 (0) | 2025.03.12 |
| 평행사변형의 대각선 길이 구하기 (0) | 2025.02.24 |
| 게임 엔진에서의 오른손 좌표계과 왼손 좌표계...그리고 오른손 법칙 (0) | 2025.02.24 |
| 게임 수학 5장-2 : 행렬(가상 세계의 변환 도구) (0) | 2023.09.08 |





