cyphen156
게임 수학 2장 : 수 (가상 세계를 구성하는 가장 작은 단위) 본문
컴퓨터가 디지털 세계를 구축하려면 어떻게 표현할까?
모든것은 좌표 평면 위에 점(Point)이 존재하는가 아닌가(참/거짓)으로 표현할 수 있고, 이 점들을 연결하면 선(Line)이, 선을 연결하면 2차원 평면도형이, 또 2차원 평면도형끼리 연결하면 3차원 입체도형의 형태가 된다.
이러한 특징은 현실에서 뿐 아니라 가상세계에서도 적용될 수 있는 법칙이고, 가상세계에서는 좀 더 쉽게 이해하기 위해 집합론을 사용한다.
집합론 (Set)
서로 구분되는 원소들을 용도에 따라 묶고, 정의하여 구분해서 사용하는 방법 정수, 자연수, 유리수, 무리수 등이 있다.
| 분류 | 정의 | 기호 |
| 자연수 | 1, 2, 3...등 0보다 큰 정수 물건을 세거나 순서를 지정하기 위해 사용한다. |
N |
| 정수 | 자연수와 자연수의 음수 0을 포함하는 수의 집합 | Z |
| 유리수 | 분모가 0이 아닌 두 정수의 비율 또는 분수로 나타낼 수 있는 수의 집합 |
Q |
| 무리수 | 1:2와 같이 두 정수 비 또는 분수로 나타낼수 없는 수의 집합 |
I |
| 실수 | 유리수와 무리수를 포함하는 수의 집합 | R |
| 허수 | 제곱하면 -1이 되는 수의 단위 | |
| 복소수 | 실수와 제곱하면 -1이 되는 허수 단위 i를 조합해서 a + bi의 형태로 표현하는 수의 집합 (a, b는 실수) | C |
| 사원수 | 복소수가 a + bi였다면 3차원 공간에서의 x, y, z축의 회전을 표현하기 위해 세 가지의 허수를 곱해 만든 복소수 a + bi + cj + dk의 형태로 표현되는 수의 집합 (a, b, c, d는 실수), i, j, k는 세 허수 |
H |

대부분 의무교육(중/고등)학교때 배웠던 것이다.
그런데 마지막에 이상한게 하나 끼어있다.
'사원수?' '저건뭐지??'
간단히 말하면 사원수는 행렬(2차원 배열)만으로는 3차원 물체의 이동, 회전등의 변형을 표현하기 어렵기 때문에 도입된 개념이다. 3차원에서는 X축, Y축, Z축 총 세가지의 베이스를 두고 점(Point)의 이동을 표현하는데 이것을 쉽게 표현하기 위함이라는 것이다.
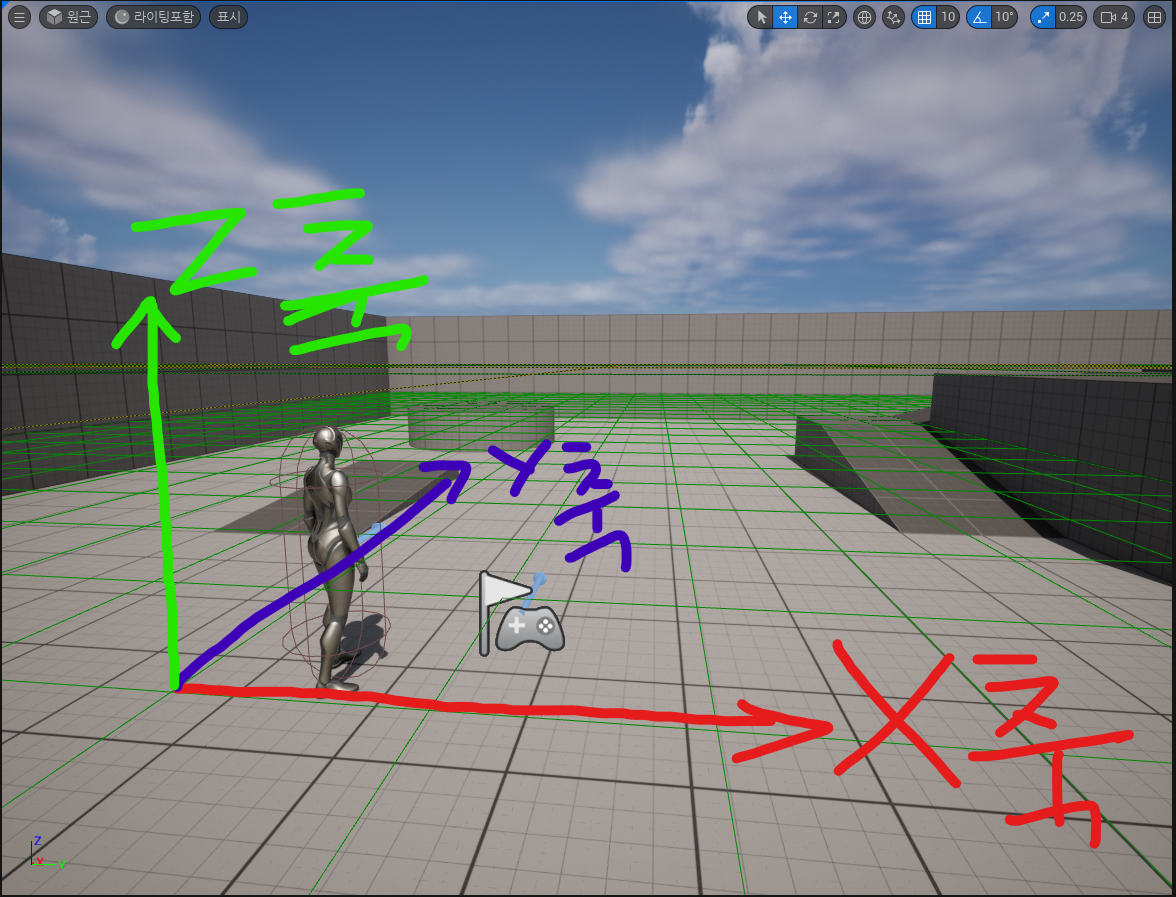
보고 있는시선에 따라 조금씩 달라질 수는 있지만 대개 x축은 좌, 우 이동을, y축은 앞, 뒤로의 이동을, z축은 상, 하로의 위치 이동을 결정한다.
여기서 사람을 각 축마다 30º 씩 회전시키면 어떻게될까?
조금 모양이 이상하긴 하지만 얼추 이런 모양이 될 것이다.
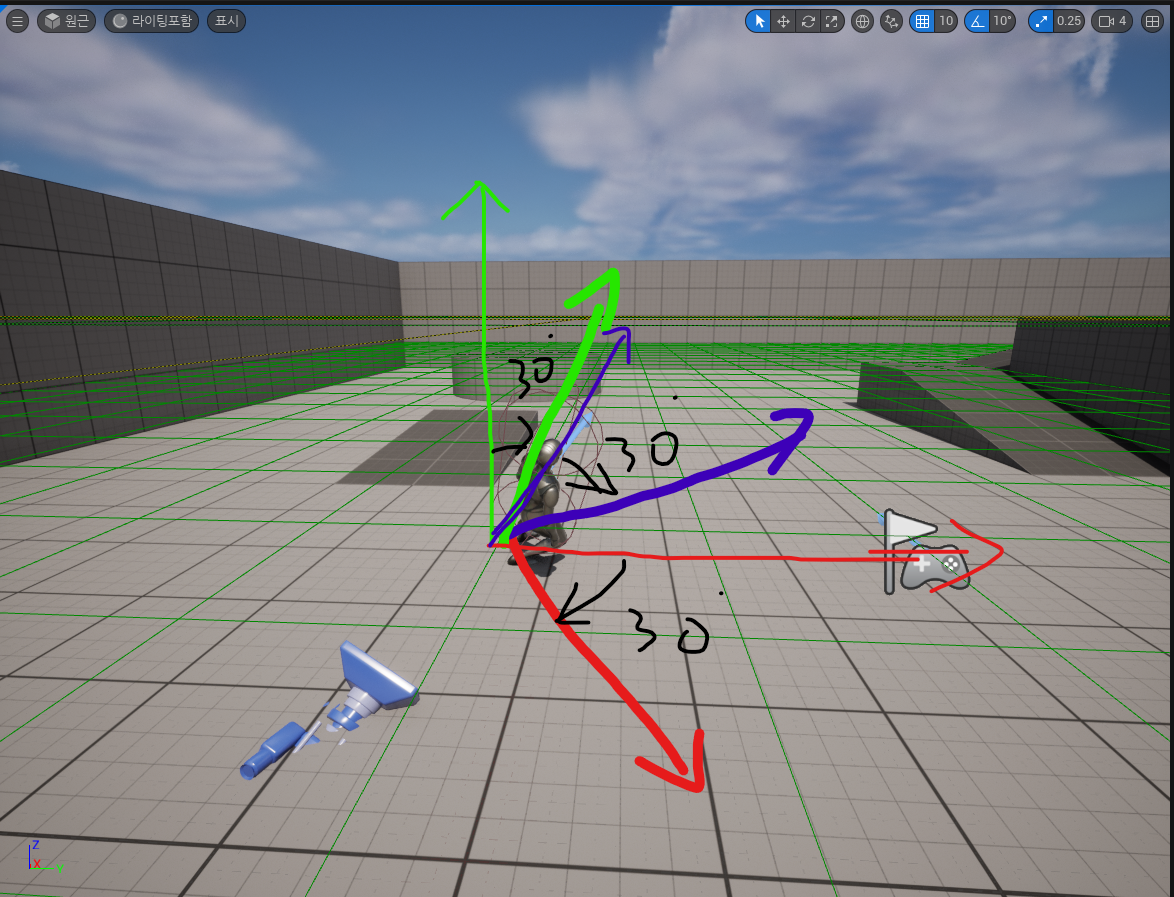
이렇게 물체의 회전을 표현하기 위해 사용되는것이 사원수다!
그런데 가상세계는 우리가 볼수는 있지만 실제로 만질 수 없는 미지의 세계이다.
그래서 우리는 이런 가상 세계의 특징을 구분짓기 위해 참거짓으로 명확하게 구분하기 위해 명제를 사용한다. 그리고 명제들 중 증명할 필요가 없는 가장 기본적인 참 거짓이 명확한 것을 공리(Axiom)라고 한다.
이제 우리는 가상공간을 표현하기 위해 집합론이라는 것을 사용하고, 이 집합의 성질을 구분하기 위해 명제를 쓴다는 것도 배웠다.
그럼 이렇게 구분지은 집합의 성질을 어떻게 이용할까?
정답은 바로 연산이다.
기본적으로 덧셈, 뺄셈, 곱셈, 나눈셈 등 두 원소를 이용해 새로운 원소를 만들어내는 연산인 이항연산(Binary Operation)이 있고, 이 이항연산을 응용해 만든 다항식, 미지수를 이용해 결과값을 도출해내는 함수(Function/f(x))가 있다.
우선 이항연산을 할 때 같은 집합(ex) A, B 두 수는 자연수)에 속한 두 항(A, B)에 대해 연산한 결과(A + B)의 값(=C)이 항상 같은 집합에 속한다면 이항연산은 해당 집합에 대해 닫혀있다고 한다.
이항연산) 자연수 + 자연수 = 자연수 면 닫혀있다는 것이다.
그리고 이항연산은 항상 교환법칙, 결합법칙, 분배법칙이 성립하고, 항등원1과 역원2이 존재한다는 것이다.
이항연산의 성질
- 닫혀 있다.
- 교환법칙이 성립한다.
- 결합법칙이 성립한다.
- 항등원이 존재한다.
- 역원이 존재한다.
- 분배법칙이 성립한다.(공리에서 제외)
이에 대한 자세한 설명은 이분이 잘 설명하신것 같아서 링크를 드립니다.
[게임 수학] #1 | 수(Numbers)의 구조 (tistory.com)
[게임 수학] #1 | 수(Numbers)의 구조
인프런 강의를 듣고 필기한 글입니다. 목차 수의 시각화 수(Number)에 대해서 알아야 하는 이유 게임 세계는 벡터(Vector)로 구성된 탄탄한 시스템을 기반으로 함. 해당 시스템 위에서 컨텐츠가 만들
daekyoulibrary.tistory.com
그런데 공리 체계에서 수집합과 이항연산을 분석하면 덧셈과 곱셈은 공리를 모두 만족시키지만 뺄셈과 나눗셈은 공리를 만족시키지 못합니다. 뺄셈과 나눗셈은 교환법칙이 성립하지 않기 때문입니다. 그래서 항상 컴퓨팅의 연산에서는 공리를 만족시키기 위해 뺄셈과 나눗셈을 음수의 덧셈과, 역원의 곱셈으로 변환하여 연산을 진행합니다.
체(Field)
위에서 이항 연산에 대해 하나의 연산만을 공리의 체계에서 분석해보았습니다. 만약 서로 다른 연산(덧셈 + 곱셈)이 2번 이루어지면 어떨까요?
앞서 이항연산의 성질을 이용하여 공리성을 판단하였습니다. 이것을 확장하여 두 연산에 대해
덧셈에 대한 성질:
- 닫혀 있다: 두 개의 요소를 더하면 그 결과도 그 집합 내에 있다.
- 교환법칙이 성립한다: a + b = b + a.
- 결합법칙이 성립한다: (a + b) + c = a + (b + c).
- 항등원이 존재한다: a + 0 = a.
- 역원이 존재한다: a + (-a) = 0.
곱셈에 대한 성질:
- 닫혀 있다: 두 개의 요소를 곱하면 그 결과도 그 집합 내에 있다.
- 교환법칙이 성립한다: a * b = b * a.
- 결합법칙이 성립한다: (a * b) * c = a * (b * c).
- 항등원이 존재한다: a * 1 = a.
- 역원이 존재한다: a * (1/a) = 1, 단, a ≠ 0.
그리고 이 두 연산은 분배법칙을 만족해야 합니다. 분배법칙: a * (b + c) = a * b + a * c.
이러한 속성을 만족하면 이것을 우리는 '체(Field)'라고 부릅니다.
수의 표현
그러면 수를 시각화 하는건 어떻게 할까?
물체의 이동은 가장 단순하게 생각하면 수직선에서의 점의 이동으로 나타낼 수 있고, 다른 좌표(Point)를 추가해가면서 차원을 높여 표현할 수 있다.((X) -> (X, Y) -> (X, Y, Z))
1차원과 2차원 표현
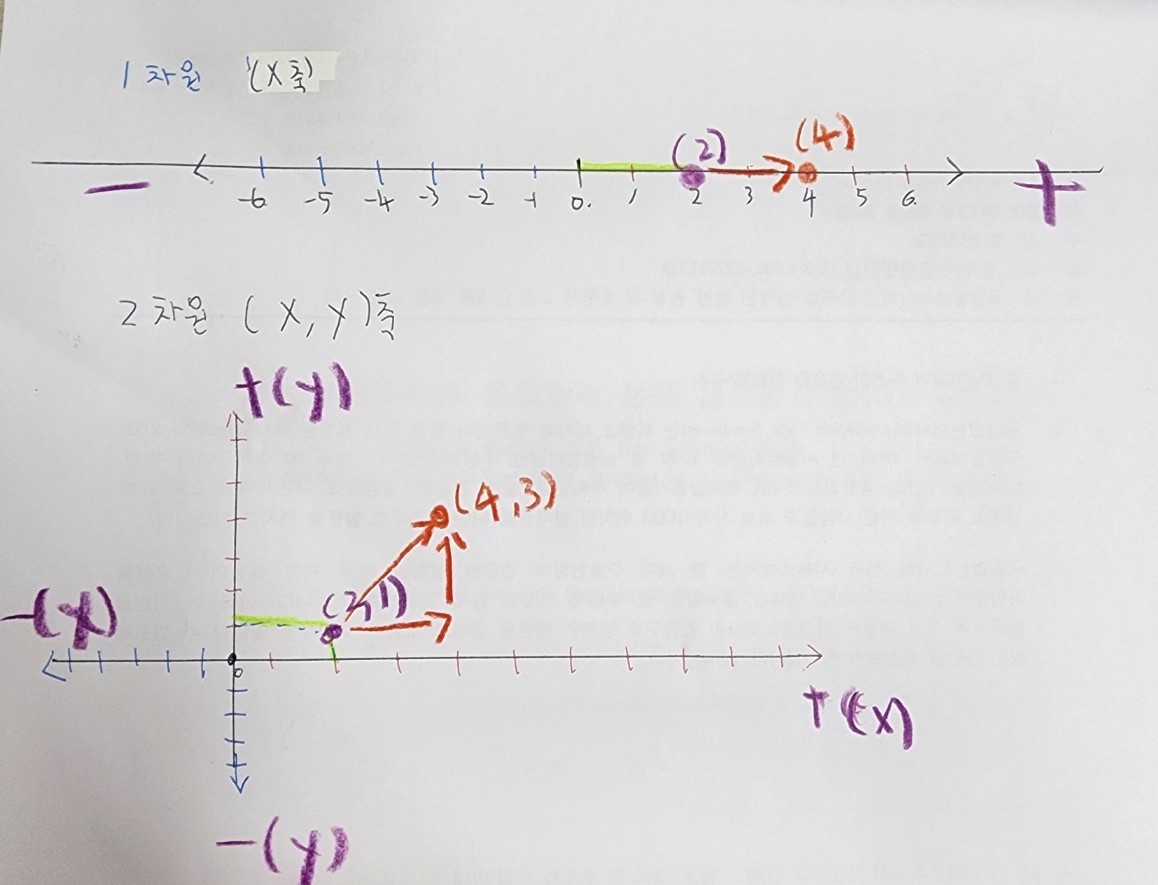
3차원 표현

그림으로 그리면 이렇게 표시가 됩니다.
함수(Function)
미지수와 함께 많은 사람들이 수학을 포기하게 만드는 원인 중 하나인 함수입니다.
저 또한 미지수 때문에 수학을 포기했엇고, 나중에 기하(그래프 표현)에 흥미를 느껴 다시 수학공부를 시작하게 되면서 이해된 것이 함수입니다.
제 생각에는 사실 그림으로 한번 그려보면 엄청 간단한데 직접 그려보지 않고 머릿속으로 암산하려해서 어려웠던것 같습니다.
다시 돌아와서
어떠한 변수(x)를 수식이라는 계산기에 넣었을 때 튀어나오는 결과를 의미하는것이 함수 f(x)라 하고, 그 결과를 y라고 합니다. 수식으로 표기하면 y = f(x)가 됩니다.
중요한 것은 어떤 x를 함수에 넣었을 때 결과가 항상 같아야 하고, 이 결과는 여러개여선 안된다는 겁니다.
함수에 대한 자세한 설명은 이산수학에서 하겠습니다.
올바른 함수의 대응관계
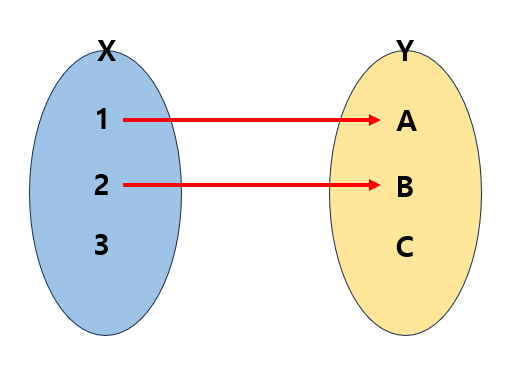
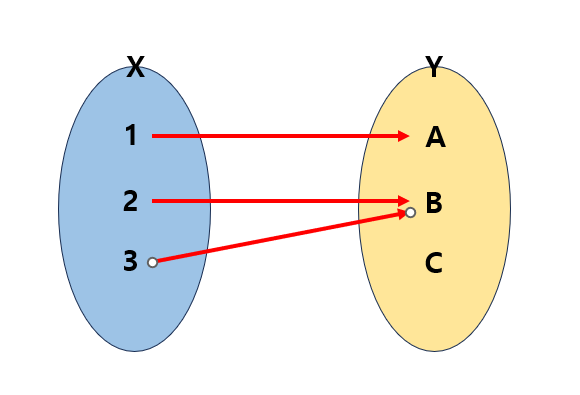
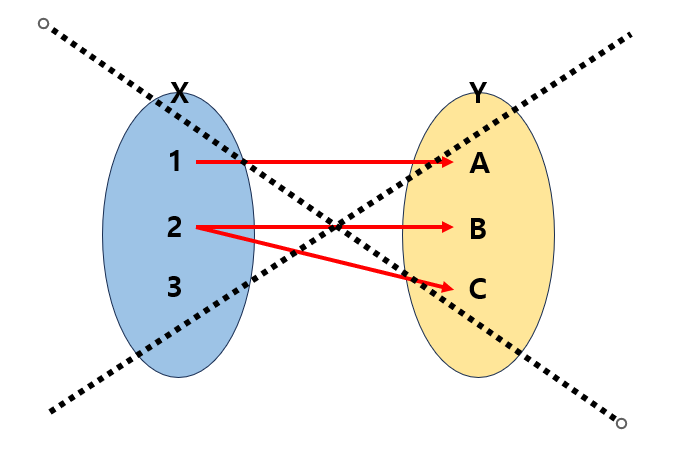
함수가 아닌 두 집합의 대응관계
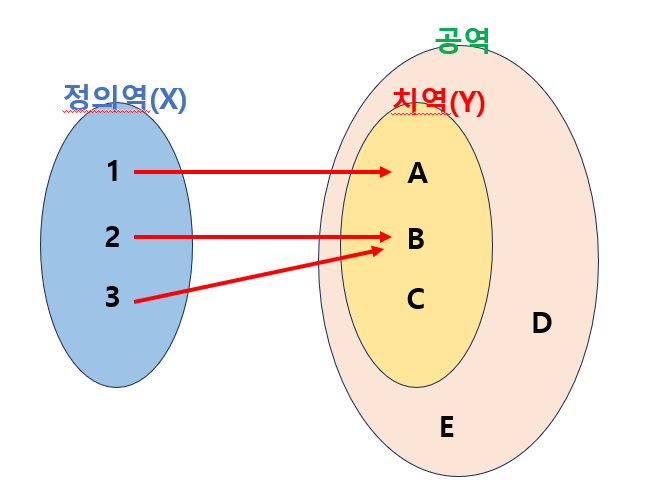
정의역, 공역, 치역
함수에는 정의역과 공역, 그리고 치역이 있습니다
정의역은 x에 해당하는 계산기에 들어가는 인자들을 말하고,
공역은 함수의 결과로 나올 수 있는 모든 수,
치역(값)은 공역에 있는 수들 중 정의역을 함수에 넣었을 때 나오는 결과로 형성되는 공역의 부분집합입니다.
함수에는 여러 종류가 있습니다.
- 전사함수(Surjection) : 공역이 곧 치역이 되는(공역의 모든 요소가 정의역에 대응되는) 함수입니다.
- 단사함수(Injection) : 정의역의 모든 요소가 공역의 요소에 일대일로 대응되는 함수입니다. 서로 다른 정의역을 함수에 넣었을 때 결과가 같을 수 없다는 뜻입니다.
- 전단사함수(Bijection) : 전사함수와 단사함수의 특징을 모두 가지고 있는 함수입니다.
- 합성함수 : 함수의 결과가 다른 함수의 정의역이 되는 중첩함수, 여러개의 함수가 연쇠적으로 계산될 때(Filed와 비슷함)를 말합니다.(g º f)(x) 또는 g(f(x))로 표현합니다.
- 항등함수(Identity) : 입력과 결과가 항상 같은 함수 x == y, id라 표현합니다.
- 역함수(Inverse) : 결과에서 입력을 도출해 내기 위한 함수의 역산, 결과를 함수에 집어넣으면 입력(정의역)이 결과로 도출됩니다. f(x) = y가 함수라면 역함수 f ̄(y) = x가 됩니다.
※ 함수에 대한 자세한 내용은 이산수학에서 다루겠습니다.
'수학/이산수학' 카테고리의 글 목록 (tistory.com)
'수학/이산수학' 카테고리의 글 목록
Cyphen의 개인 공부 블로그입니다. 프사는 아는 동생이 그려준 그림 주인장과 싱크로율 0%
cyphen156.tistory.com
곱집합과 좌표평면
마지막으로 이야기 할 것은 곱집합과 좌표평면에 대한 이야기입니다.
엑셀을 이용해서 설명해보겠습니다
A와 B라는 두 개의 집합(Set)이 존재할 때, 이 두 집합을 곱하면 A X B라는 크기의 배열이 생깁니다.
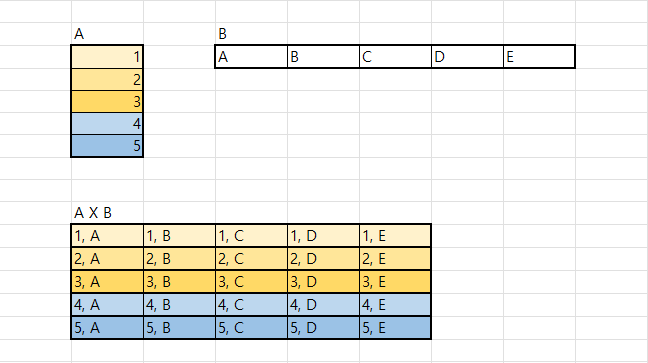
"어? 어디서 많이 봤는데???"
네 맞습니다. 수의 표현 중 2차원에 해당하는 그림이네요
이것을 다시한번 곱집합을 하면 3차원이 될것 같네요.
이제 2장에 대한 내용 공부가 끝났습니다. 엄청오래걸렷네요ㅜㅜ
이게다 주인장이 게을러서 그렇습니다.
다음에 다룰 내용은 벡터에 대한 내용입니다.
이과생들도 포기한다는 그 벡터요..!!
무튼 얼마나 걸릴지는 모르겟지만 최선을 다해 공부해보도록하죠.
모든 예제 코드의 소스파일은 GitHub - onlybooks/gamemath: <이득우의 게임 수학> 공식 깃허브 페이지
GitHub - onlybooks/gamemath: <이득우의 게임 수학> 공식 깃허브 페이지
<이득우의 게임 수학> 공식 깃허브 페이지. Contribute to onlybooks/gamemath development by creating an account on GitHub.
github.com
또한 제 개인 깃허브 레포지토리 에 있습니다.
'수학 > 게임수학' 카테고리의 다른 글
| 게임 수학 5장-2 : 행렬(가상 세계의 변환 도구) (0) | 2023.09.08 |
|---|---|
| 게임 수학 5장-1 : 선형성 (0) | 2023.08.22 |
| 게임 수학 4장 : 삼각함수(회전을 위한 수학) (0) | 2023.08.18 |
| 게임 수학 3장 : 벡터(가상 공간의 탄생) (1) | 2023.08.17 |
| 게임 수학 1장 메타버스를 지탱하는 게임 수학 (0) | 2023.05.17 |





