cyphen156
게임 수학 4장 : 삼각함수(회전을 위한 수학) 본문
앞서 배웠던 벡터 공간에서 그려진 물체를 이동시킬때는 벡터의 덧셈과 곱셈을 이용해 직선 상의 움직임을 통해 표현하였습니다. 이제 4장에서는 벡터 공간에서의 물체의 회전 이동을 표현하기 위해 원을 그리고, 이 궤적을 따라 점(Point)을 이동시키기 위해 삼각함수에 대해 알아야 합니다.
삼각함수
고등학교때 배웠던 내용을 끄집어 내보면 뭐였는지 하나도 기억안나는 삼각비에 대한 내용 [얼싸안고(All, Sin, Tan, Cos)], 피타고라스의 정리(빗변과 끼인 각, 직각과의 관계)등이 있었던 것 같습니다.
삼각함수의 기본은 피타고라스의 정리입니다.
1피타고라스의 정리는 직각삼각형을 이루는 세 변(빗변, 밑변, 높이)사이의 관계[밑변과 높이, 그리고 둘 사이의 끼인 각(90˚ / 직각)과 빗변 사이의 관계]에 대한 정리입니다.
삼각형
도형에서 존재하는 모든 각의 수가 3개이고, 이 각들의 합이 180˚(π)인 도형을 삼각형이라고 합니다.
삼각비
- 빗변(Hypotenuse)
- 밑변(Adjacent)
- 높이(Opposite)
앞선 장에서 간단하게 피타고라스의 정리에 대해서 이야기하고, 피타고라스의 정리를 통해 이차원 벡터 공간에서의 특정 벡터의 크기를 계산했었습니다.
이제 이 피타고라스의 정리를 응용하여 삼각비에 대해 배워야 합니다.
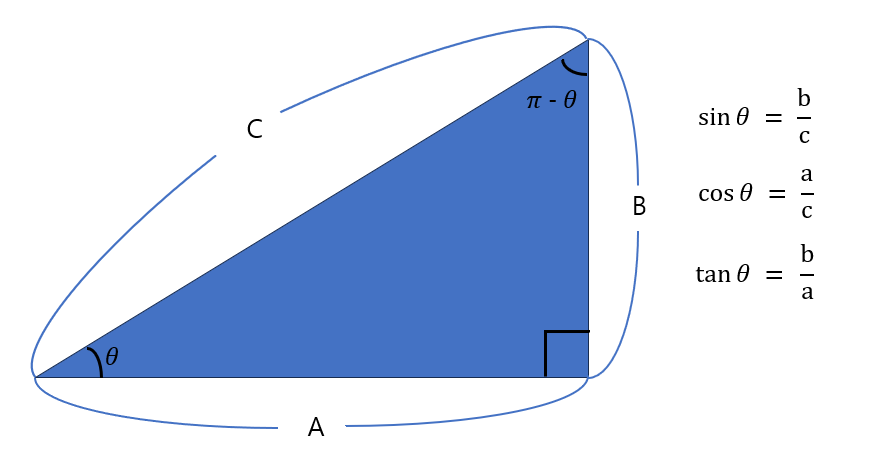
이 그림을 데카르트 좌표계에서 반지름(r)이 1인 단위 원을 사용해서 나타내면
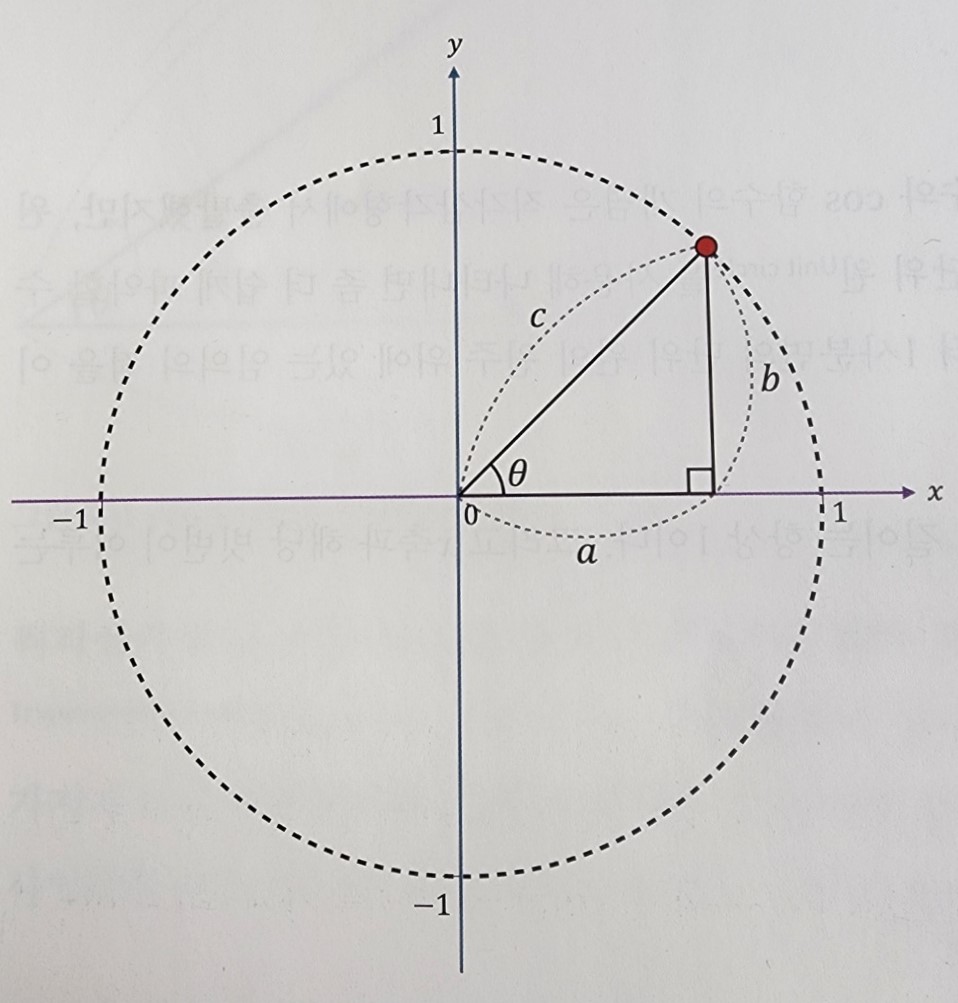
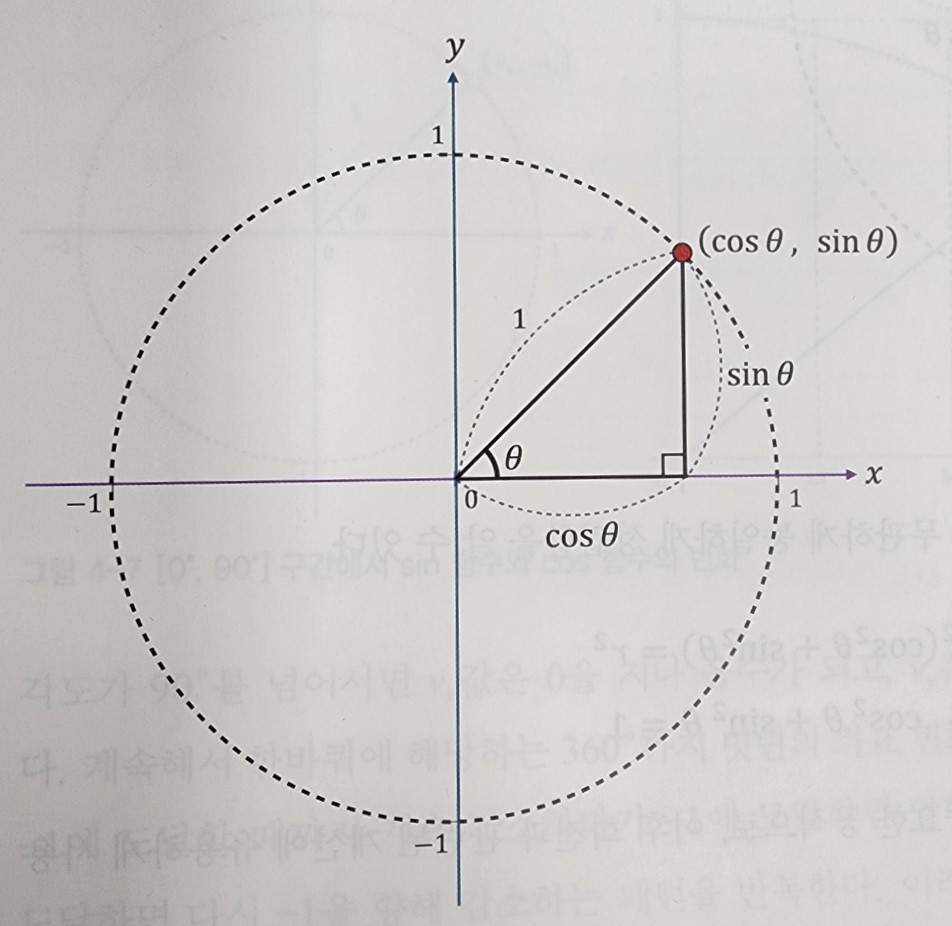
다음과 같은 형태로 표시할 수 있습니다.
여기서 c=n이라 가정하면 밑변 a의 길이는 ncosθ, 높이 b의 길이는 nsinθ가 됩니다.
다시 말하면 단위 원에서는 sin²θ+cos²θ=1², n²sin²θ+n²cos²θ=n²라는 빗변의 길이 공식이 도출된다는 것입니다.
위에서 나왔던 삼각비를 약간 변형하면 다시 삼각형의 각 변의 길이를 구할 수 있습니다.
높이 b는 c * sinθ, 밑변 a는 c * cosθ, 빗변 c는 b / sinθ = a / cosθ로 나타낼 수 있습니다.
삼각함수의 성질
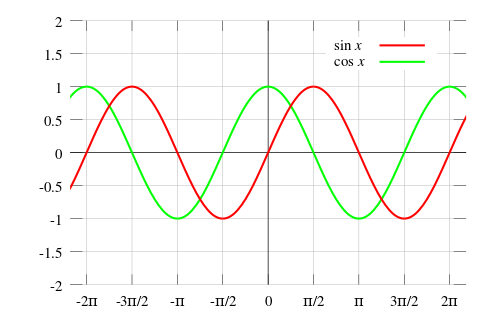
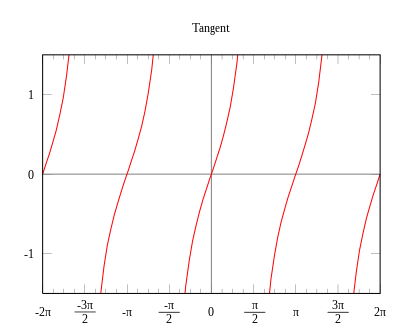
출처 : 삼함수 - 위키백과, 우리 모두의 백과사전 (wikipedia.org)
여기서 π는 180˚라고 했었습니다. 기억해야 할 점은 2π라는 주기를 갖고 그래프가 반복되고 있으며, x축을 기준으로 cos그래프는 좌우 대칭을, sin과 tan그래프는 원점을 중심으로 대칭을 이루고 있다는 것, 그리고 sin과 cos그래프의 관계는 서로를 +90˚(π/2) 또는 270˚(π * 3/2)만큼 대칭 이동시킨 결과라는 것과 tan그래프는 예외적으로 π주기를 갖고 반복되고 있으며, 그 값이 순회하지 않는 극한에 수렴하는 값이라는 것과, 각 주기가 서로 만나지 않는다는 것(이어지지 않는 그래프)입니다.
정리하자면 다음과 같습니다.
- π = 180˚
- sin함수과 cos함수는 2π를 주기로 반복한다.
- tan함수는 π를 주기로 반복한다.
- sin함수과 cos함수는 항상 -1부터 1사이의 값을 갖는다. == [-1, 1]의 진폭을 갖는다.
- tan함수는 π/2, π * 3/2의 각도에서 +-로의 극한값을 갖는다. 왜냐하면 분모가 0인 경우는 존재하지 않기 때문이다.
- sin함수는 cos함수를 +π/2만큼 평행이동한 것과 같다.
- cos함수는 x축을 기준으로 좌우 대칭이며, 이를 짝함수 또는 우함수라고 부른다.(cos(-θ) = cosθ)
- sin함수와 tan함수는 원점(0, 0)을 기준으로 대칭이며, 이를 홀함수 또는 기함수라고 부른다. sin(-θ) = -sinθ
- tanθ는 b/a 즉, sinθ / cosθ == (b/c) / (a/c)이다.
각의 측정
각도법
각도법은 원을 ˚(도)라는 단위를 이용해 360개로 쪼개어 표현하는 방법입니다.
왜 360개냐 하면 360이라는 수가 약수가 많이 나오는 수이기 때문에 사용했다고 합니다.
호도법
호도법은 360이라는 너무 큰 수가 아닌 일상생활에서 사용하기 편한 단위인 π(1radian = 180˚/π == 57.29....)를 기준으로 각을 측정하여 표시한 것입니다.
물체의 회전
벡터 공간에서의 물체가 θ만큼 회전했을 때 렌더링될 좌표의 연산은 단위 원을 기준으로 기저벡터를 활용하여 계산합니다.
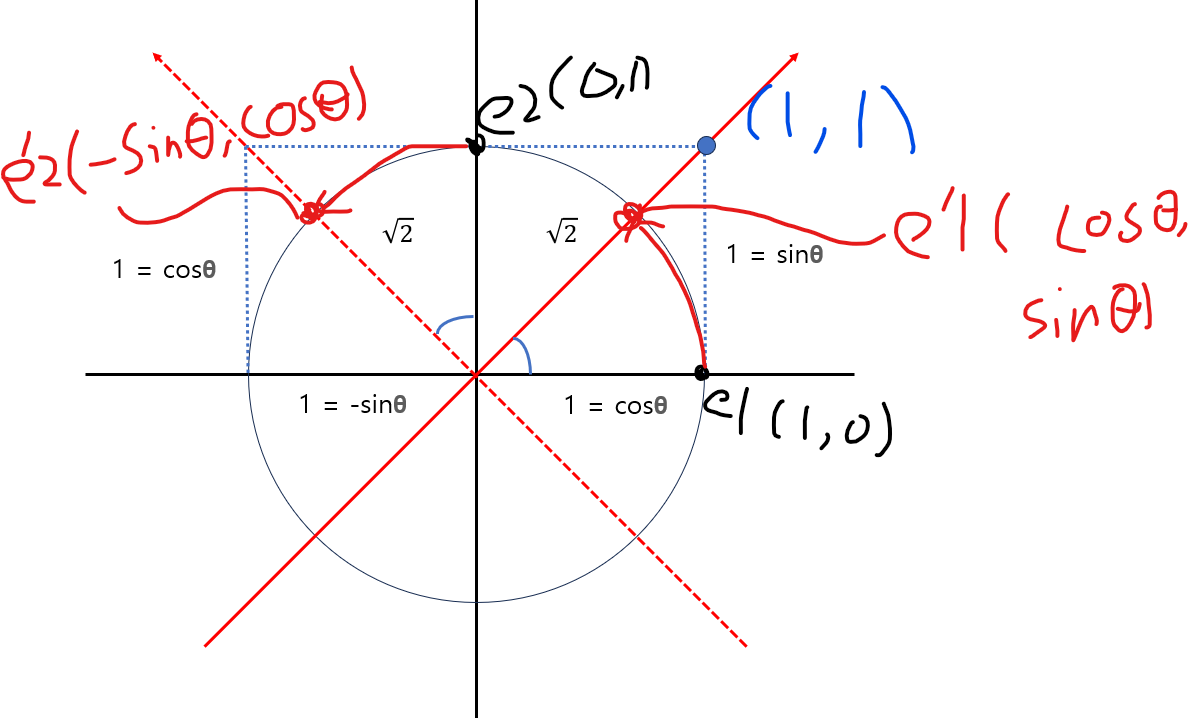
여기에서 e1과 e2의 길이는 각각 √(1*1 + 1*1) = √2이고, 좌표는 (1, 1), (-1, 1)입니다 여기서 e1을 회전하여 v'으로 이동시킨다고 할때
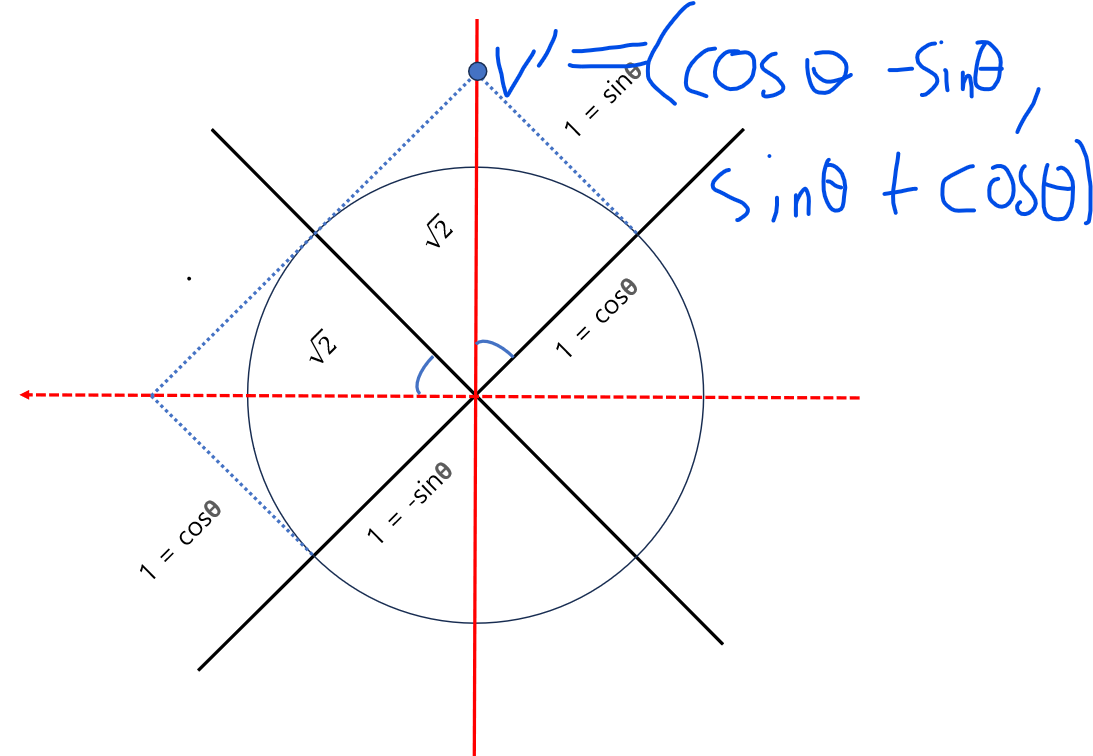
단순히 회전만 시킨다고 보면 이런 그림이 될 겁니다.
여기서 v'의 길이는 √2, 좌표는 (0, √2)가 될겁니다.
이 좌표를 도출하기 위한 수식은
v-> = 1 * e1(1, 0) + 1*e2(0, 1),
v'-> = 1 * e'1(cosθ, sinθ) + 1*e'2(-sinθ, cosθ)가 될 겁니다.
다시말하면 v'->의 좌표는 (cosθ-sinθ, sinθ + cosθ)가 될 겁니다. 단위원을 기준으로 결론을 도출했으니 일반화 한 식은
x' = xcosθ - ysinθ
y' = xsinθ + ycosθ이 됩니다.
삼각함수의 역수
삼각함수에는 역원이 존재합니다
- sin의 역원 1/sin은 csc(코시컨트)
- cos의 역원 1/cos는 sec(시컨트)
- tan의 역원은 1/tan인데 tan은 cos/sin으로 표기할 수 있으니 sin/cos로 cot(코탄젠트)
삼각함수의 역함수
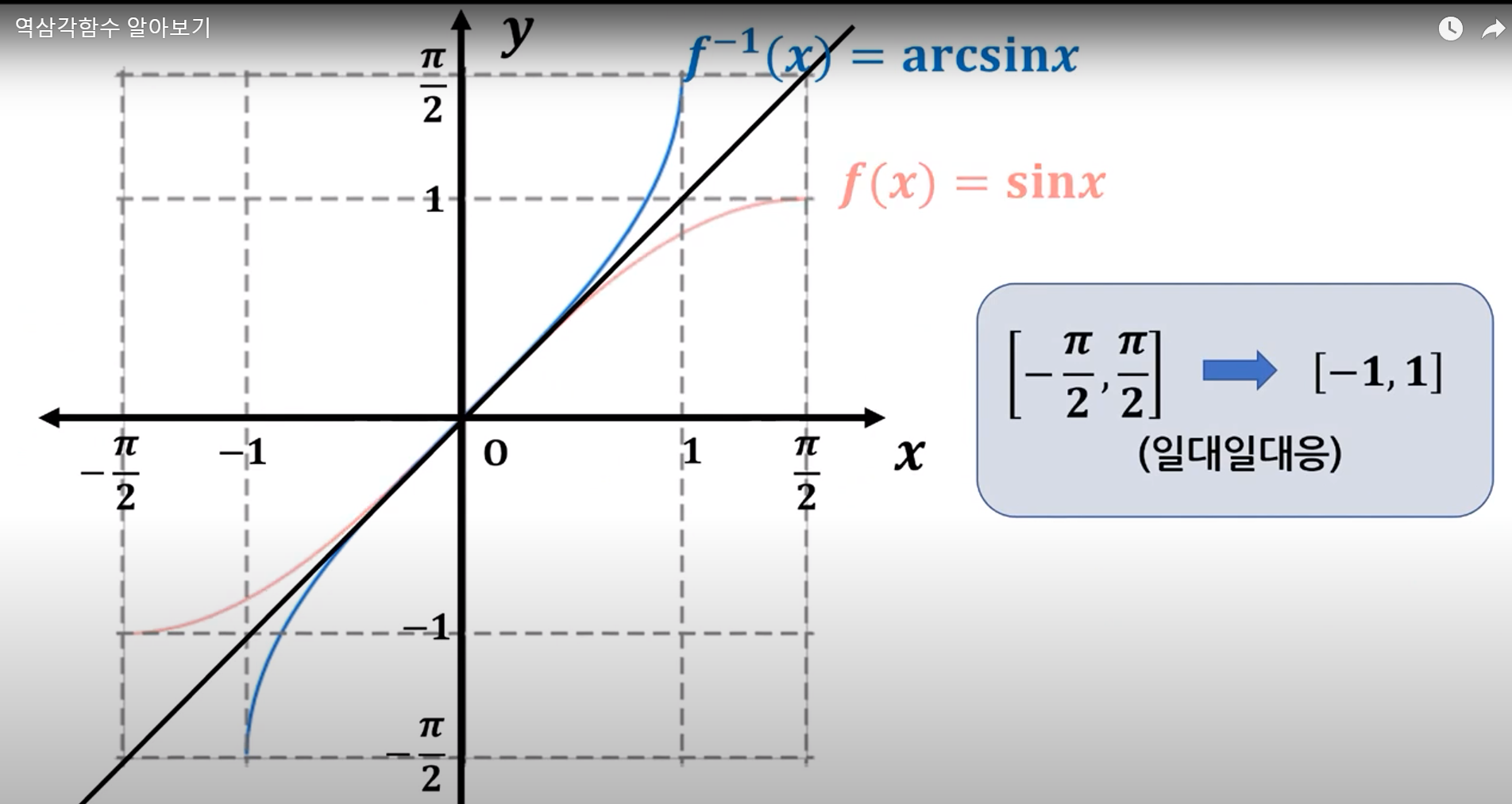
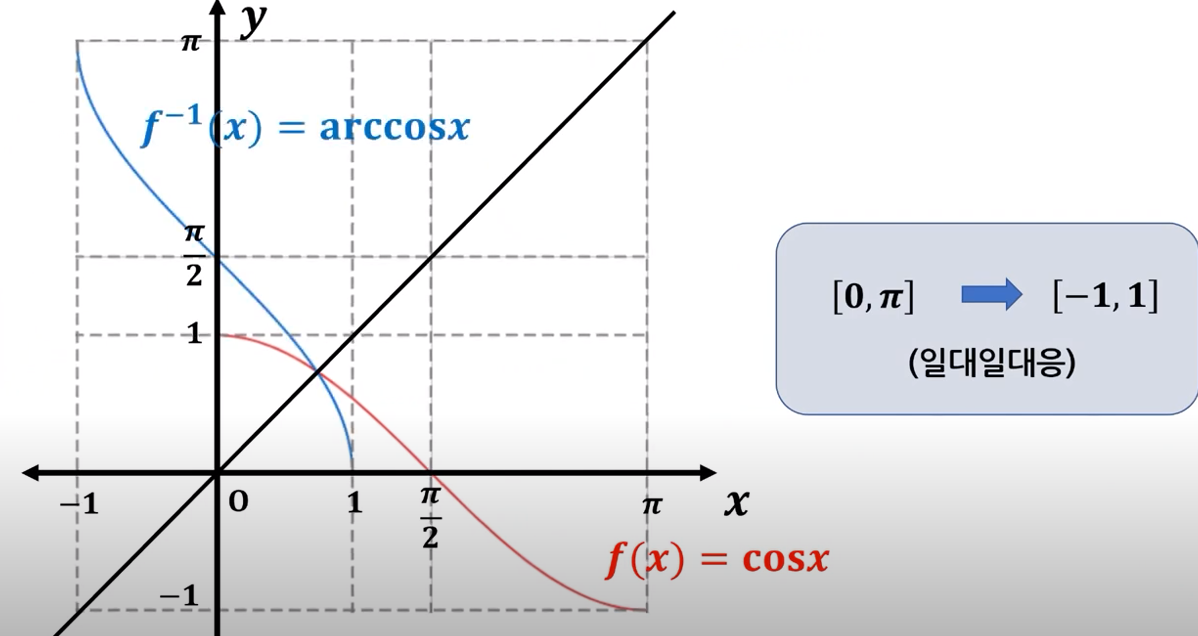
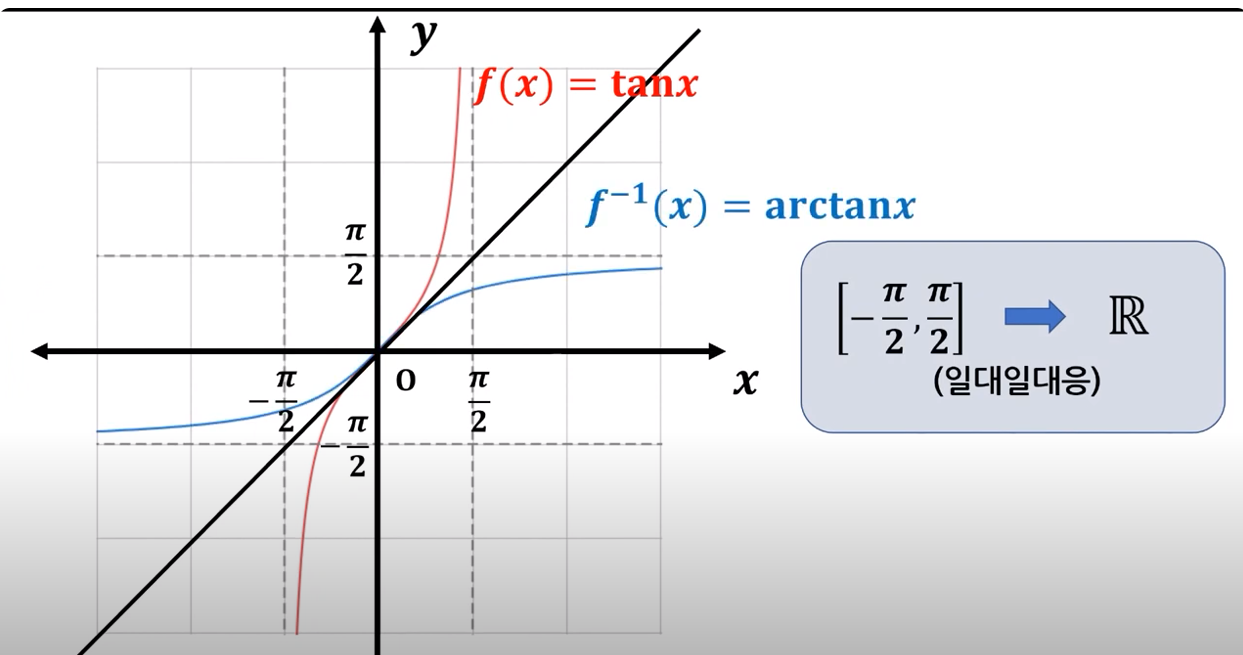
삼각함수의 역함수를 아크(arc)함수라고 부릅니다.
아크함수는 각 삼각함수마다 arcsin, arccos, arctan로 불립니다.
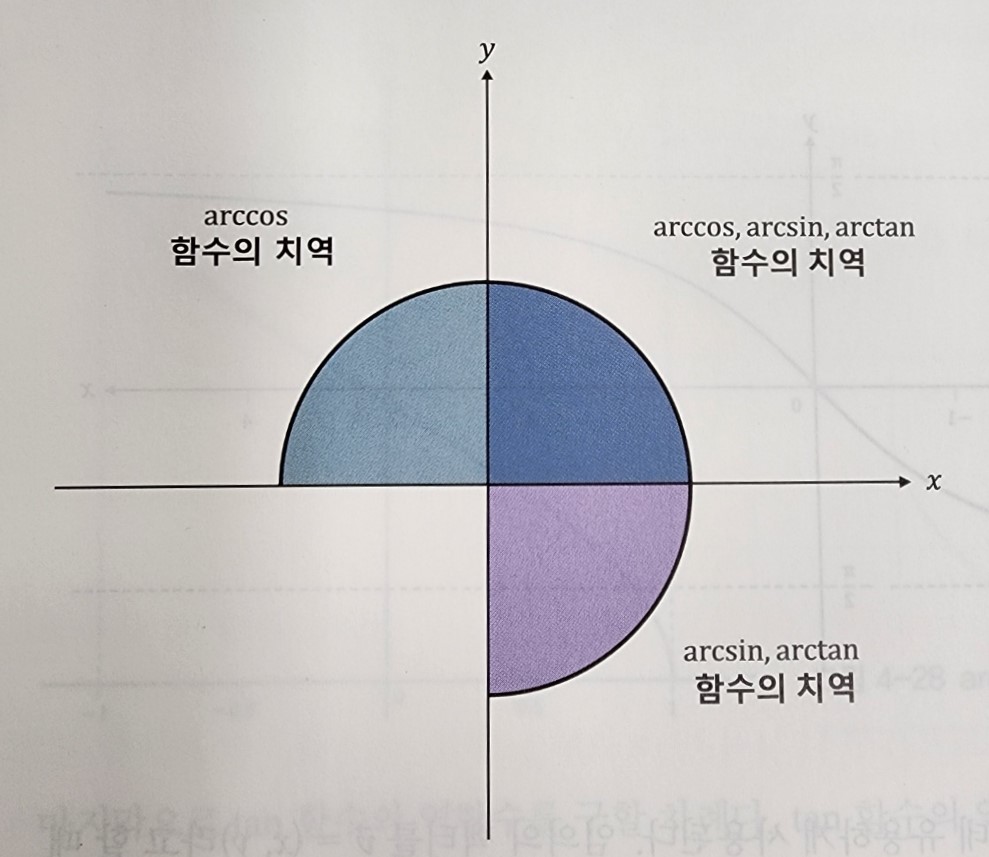
하지만 삼각함수는 일정 주기마다 반복되기 때문에 전단사함수로 만들기 위해 범위를 제한하면 [-90˚, 90˚](sin, tan)또는 [0˚, 180˚](cos)사이의 값만을 공역으로, [-1, 1]치역으로 설정하여 역함수를 구한다면
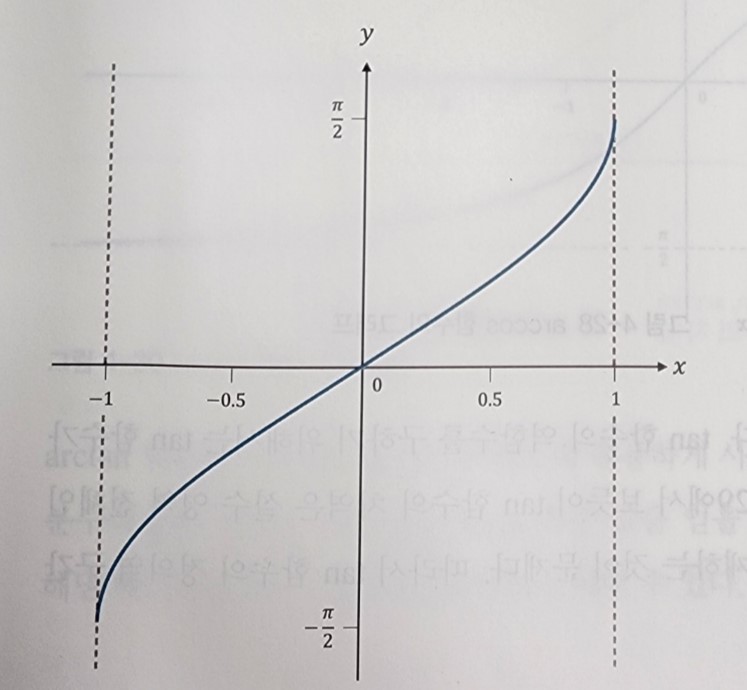
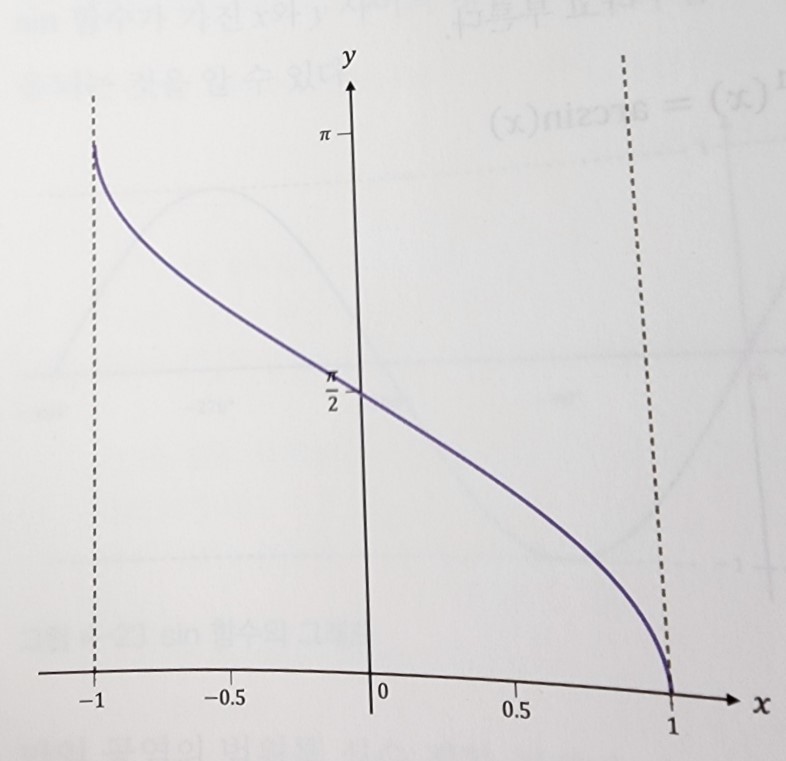
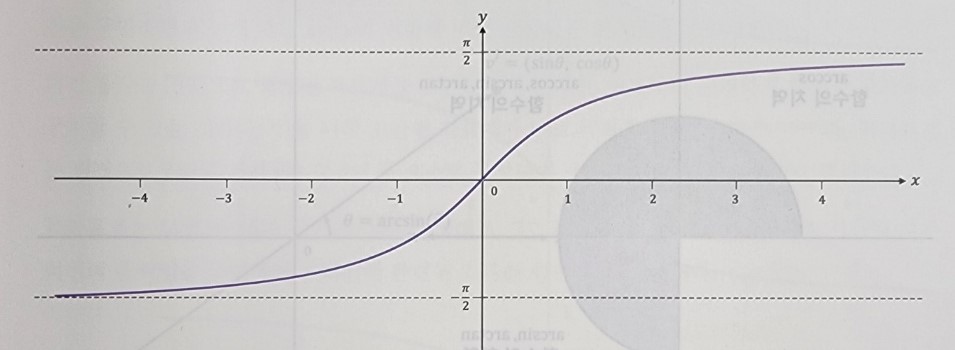
그런데 분모에는 0이 올 수 없으므로 역함수를 통해서 얻을 수 있는 각은 범위에 제한이 존재한다. 바로 3사분면에 위치한 값에 대한 정보는 얻을 수 없다는 것입니다.
그래서 acrtan함수를 응용하여 인자값에 y/x를 전달하는 것이 아닌 따로 분리하여 x와 y 두 인자를 전달하면 4사분면 전체 범위에 해당하는 각의 정보를 얻을 수 있습니다.
즉, arctan함수의 치역의 범위를 [-90˚, 90˚]에서 [-180˚, 180˚]로 확장하여 두 인자를 각각 다른 그래프에 적용시켜 표현하는것 입니다.
이를 acrtan2(y, x) = atan2(y, x)
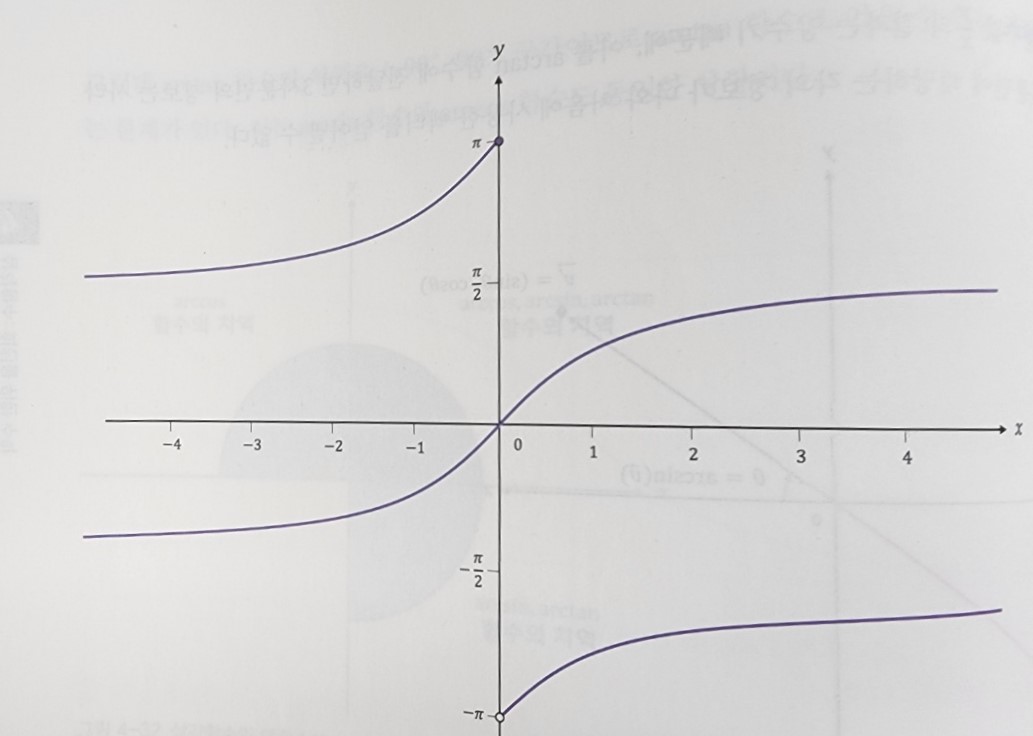
다음 유튜브 링크를 통해 자세하게 그림으로 확인할 수 있다.
https://www.youtube.com/watch?v=5jynGqXMW_E
극좌표계
물체를 이동시키고 크기를 늘리는 동작은 x와 y가 독립적으로 적용되는 움직임인데 반해 회전은 두 변수가 함께 영향을 받는 동작입니다. 따라서 회전 움직임을 연산시 매번 x와 y의 변화를 계산하는 번거로움이 있습니다.
이걸 편하게 관리할 수 있지 않을까? 라는 고민에서 나온 결과가 극좌표계라는 체계입니다.
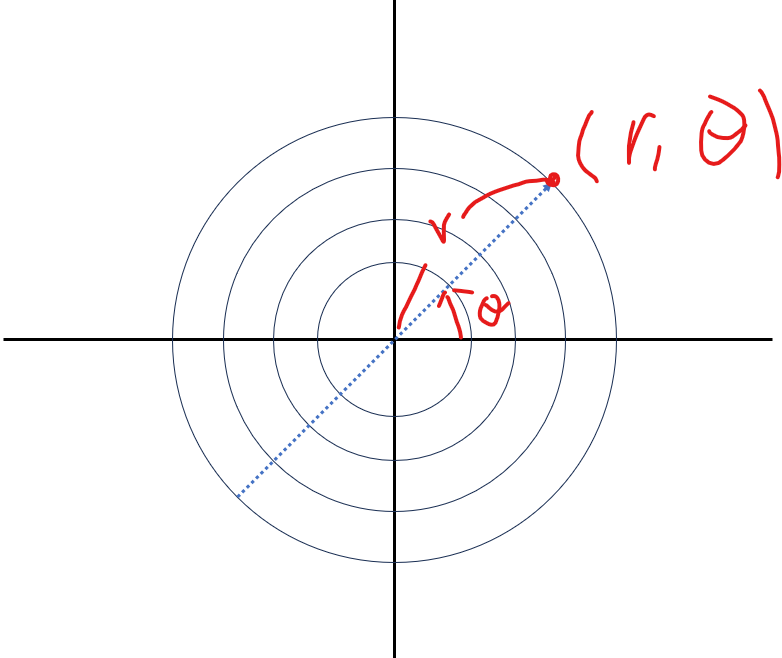
r은 x² + y²의 제곱근이고, θ는 atan2(y, x)입니다.
다음에 배울 내용은 행렬에 대한 내용입니다. 이산수학과 같은 과목에서도 배우겠지만 챕터에 있는 내용이고, 컴퓨터 공학의 핵심적인 내용을 다룰 수 있으므로 여기서도 나름대로 정리해보겠습니다.
실습하기
다음의 코드는 본문 내용중 CH4 삼각함수 : 회전을 위한 수학 내의 예제 코드 1~5까지를 모두 합친 코드입니다.
중간에 하트를 색칠하는 부분은 chatgpt4의 도움을 받아 완성하였습니다.
- Home/End버튼을 통해 하트그래프와 사각형 그래프를 "회전"시킬 수 있습니다
- 화살표 키를 입력하여 하트그래프를 평행이동 시킬 수 있습니다.
- 하트 그래프는 일정 주기를 반복하며 펌핑(커졋다/작아졋다)를 반복하고, 펌핑시 그래프 안의 영역이 색칠되거나 빈 공간으로 표현됩니다.
#include "Precompiled.h"
#include "SoftRenderer.h"
#include <random>
using namespace CK::DD;
// 격자를 그리는 함수
void SoftRenderer::DrawGizmo2D()
{
auto& r = GetRenderer();
const auto& g = Get2DGameEngine();
// 그리드 색상
LinearColor gridColor(LinearColor(0.8f, 0.8f, 0.8f, 0.3f));
// 뷰의 영역 계산
Vector2 viewPos = g.GetMainCamera().GetTransform().GetPosition();
Vector2 extent = Vector2(_ScreenSize.X * 0.5f, _ScreenSize.Y * 0.5f);
// 좌측 하단에서부터 격자 그리기
int xGridCount = _ScreenSize.X / _Grid2DUnit;
int yGridCount = _ScreenSize.Y / _Grid2DUnit;
// 그리드가 시작되는 좌하단 좌표 값 계산
Vector2 minPos = viewPos - extent;
Vector2 minGridPos = Vector2(ceilf(minPos.X / (float)_Grid2DUnit), ceilf(minPos.Y / (float)_Grid2DUnit)) * (float)_Grid2DUnit;
ScreenPoint gridBottomLeft = ScreenPoint::ToScreenCoordinate(_ScreenSize, minGridPos - viewPos);
for (int ix = 0; ix < xGridCount; ++ix)
{
r.DrawFullVerticalLine(gridBottomLeft.X + ix * _Grid2DUnit, gridColor);
}
for (int iy = 0; iy < yGridCount; ++iy)
{
r.DrawFullHorizontalLine(gridBottomLeft.Y - iy * _Grid2DUnit, gridColor);
}
ScreenPoint worldOrigin = ScreenPoint::ToScreenCoordinate(_ScreenSize, -viewPos);
r.DrawFullHorizontalLine(worldOrigin.Y, LinearColor::Red);
r.DrawFullVerticalLine(worldOrigin.X, LinearColor::Green);
}
// 게임 오브젝트 목록
// 최초 씬 로딩을 담당하는 함수
void SoftRenderer::LoadScene2D()
{
// 최초 씬 로딩에서 사용하는 모듈 내 주요 레퍼런스
auto& g = Get2DGameEngine();
}
// 게임 로직과 렌더링 로직이 공유하는 변수
Vector2 currentPosotion;
float currentScale = 10.0f;
float currentDegree = 0.f;
// 게임 로직을 담당하는 함수
void SoftRenderer::Update2D(float InDeltaSeconds)
{
// 게임 로직에서 사용하는 모듈 내 주요 레퍼런스
auto& g = Get2DGameEngine();
const InputManager& input = g.GetInputManager();
// 게임 로직의 로컬 변수
static float moveSpeed = 100.f;
static float scaleMin = 5.f;
static float scaleMax = 20.f;
static float scaleSpeed = 20.f;
static float duration = 1.5f;
static float elapsedTime2 = 0.f;
static float rotateSpeed = 180.f;
Vector2 inputVector = Vector2(input.GetAxis(InputAxis::XAxis), input.GetAxis(InputAxis::YAxis)).GetNormalize();
Vector2 deltaPosition = inputVector * moveSpeed * InDeltaSeconds;
float deltaScale = input.GetAxis(InputAxis::ZAxis) * scaleSpeed * InDeltaSeconds;
float deltaDegree = input.GetAxis(InputAxis::WAxis) * rotateSpeed * InDeltaSeconds;
elapsedTime2 += InDeltaSeconds;
elapsedTime2 = Math::FMod(elapsedTime2, duration);
float currentRad = (elapsedTime2 / duration) * Math::TwoPI;
float alpha = (sinf(currentRad) + 1) * 0.5f;
currentPosotion += deltaPosition;
//currentScale = Math::Clamp(currentScale + deltaScale, scaleMin, scaleMax);
currentScale = Math::Lerp(scaleMin, scaleMax, alpha);
currentDegree += deltaDegree;
}
// 렌더링 로직을 담당하는 함수
void SoftRenderer::Render2D()
{
// 렌더링 로직에서 사용하는 모듈 내 주요 레퍼런스
auto& r = GetRenderer();
const auto& g = Get2DGameEngine();
// 배경에 격자 그리기
DrawGizmo2D();
// 렌더링 로직의 로컬 변수
float rad = 0.f;
static float increment = 0.001f;
static std::vector<Vector2> hearts;
HSVColor hsv(0.f, 1.f, 0.85f);
// 시공의 폭풍 구현
static float halfSize = 100.f;
static std::vector<Vector2> squares;
if (squares.empty())
{
for (float x = -halfSize; x <= halfSize; x += 0.25f)
{
for (float y = -halfSize; y <= halfSize; y += 0.25f)
{
squares.push_back(Vector2(x, y));
}
}
}
// 하트를 구성하는 점 생성
if (hearts.empty())
{
for (rad = 0.f; rad < Math::TwoPI; rad += increment)
{
// 하트 방정식
// x와 y를 구하기.
// hearts.push_back(Vector2(x, y));
float sin = sinf(rad);
float cos = cosf(rad);
float cos2 = cosf(2 * rad);
float cos3 = cosf(3 * rad);
float cos4 = cosf(4 * rad);
float x = 16.f * sin * sin * sin;
float y = 13 * cos - 5 * cos2 - 2 * cos3 - cos4;
hearts.push_back(Vector2(x, y));
}
}
// 0.5초 주기로 깜빡이기
static float elapsedTime = 0.0f;
static bool isVisible = true;
elapsedTime += 1.0f / 60.0f; // 업데이트 빈도에 따라 조정 필요
if (elapsedTime >= 0.1f)
{
isVisible = !isVisible;
elapsedTime = 0.0f;
}
//각도에 해당하는 사인과 코사인값 얻기
float sin = 0.f, cos = 0.f;
Math::GetSinCos(sin, cos, currentDegree);
rad = 0.f;
for (auto const& v : hearts)
{
rad += increment;
// 1. 점에 크기를 적용
Vector2 scaledV = v * currentScale;
// 2. 크기가 변한 점을 회전
Vector2 rotateV = Vector2(scaledV.X * cos - scaledV.Y * sin, scaledV.X * sin + scaledV.Y * cos);
// 3. 회전시킨 점을 이동
Vector2 translatedV = rotateV + currentPosotion;
hsv.H = rad / Math::TwoPI;
// 윤곽선 그리기
//r.DrawPoint(v * currentScale + currentPosotion, hsv.ToLinearColor());
r.DrawPoint(translatedV, hsv.ToLinearColor());
if (isVisible) // 색칠할 부분만 isVisible 상태에 따라 그리기
{
Vector2 origin = Vector2(0, 0);
Vector2 direction = (v - origin).GetNormalize();
for (float t = 0; t <= 1; t += 0.01f)
{
Vector2 pointOnLine = origin + direction * t * v.Size();
// 1. 점에 크기를 적용
Vector2 scaledPoint = pointOnLine * currentScale;
// 2. 크기가 변한 점을 회전
Vector2 rotatedPoint = Vector2(scaledPoint.X * cos - scaledPoint.Y * sin, scaledPoint.X * sin + scaledPoint.Y * cos);
// 3. 회전시킨 점을 이동
Vector2 translatedPoint = rotatedPoint + currentPosotion;
r.DrawPoint(translatedPoint, hsv.ToLinearColor());
}
}
/*
r.PushStatisticText(std::string("Position : ") + currentPosotion.ToString());
r.PushStatisticText(std::string("scale : ") + std::to_string(currentScale));
r.PushStatisticText(std::string("Degree : ") + std::to_string(currentDegree));
*/
}
// 시공의 폭풍 구현하기
// 현재 화면의 크기로부터 길이를 비교할 기준양 정하기
static float maxLength = Vector2(_ScreenSize.X, _ScreenSize.Y).Size() * 0.5f;
// 원을 구성하는 점을 그린다.
for (auto const& v : squares)
{
// r극 좌표계 변경
Vector2 polarV = v.ToPolarCoordinate();
// 극좌표계의 각 정보로부터 색상을 결정한다.
if (polarV.Y < 0.f)
{
polarV.Y += Math::TwoPI;
}
hsv.H = polarV.Y / Math::TwoPI;
// 극좌표계의 크기 정보로부터 회전량 결정
float ratio = polarV.X / maxLength;
float weight = Math::Lerp(1.f, 5.f, ratio);
polarV.Y += Math::Deg2Rad(currentDegree) * weight;
// 최종 값을 데카르트 좌표계로 변환하기
Vector2 cartesianV = polarV.ToCartesianCoordinate();
r.DrawPoint(cartesianV, hsv.ToLinearColor());
}
}
// 메시를 그리는 함수
void SoftRenderer::DrawMesh2D(const class DD::Mesh& InMesh, const Matrix3x3& InMatrix, const LinearColor& InColor)
{
}
// 삼각형을 그리는 함수
void SoftRenderer::DrawTriangle2D(std::vector<DD::Vertex2D>& InVertices, const LinearColor& InColor, FillMode InFillMode)
{
}
모든 예제 코드의 소스파일은
GitHub - onlybooks/gamemath: <이득우의 게임 수학> 공식 깃허브 페이지
GitHub - onlybooks/gamemath: <이득우의 게임 수학> 공식 깃허브 페이지
<이득우의 게임 수학> 공식 깃허브 페이지. Contribute to onlybooks/gamemath development by creating an account on GitHub.
github.com
또한 제 개인 깃허브 레포지토리 에 있습니다.
Workspace/C++/GameMath at main · cyphen156/Workspace · GitHub
※ 이미지는 게임수학 서적 내에서 발췌했습니다.
※ 위키백과와 이득우 교수님의 인프런 게임수학강의를 참고하여 작성되었습니다.
- 피타고라스 : 고대 그리스의 수학이자 철학 [본문으로]
'수학 > 게임수학' 카테고리의 다른 글
| 게임 수학 5장-2 : 행렬(가상 세계의 변환 도구) (0) | 2023.09.08 |
|---|---|
| 게임 수학 5장-1 : 선형성 (0) | 2023.08.22 |
| 게임 수학 3장 : 벡터(가상 공간의 탄생) (1) | 2023.08.17 |
| 게임 수학 2장 : 수 (가상 세계를 구성하는 가장 작은 단위) (1) | 2023.07.13 |
| 게임 수학 1장 메타버스를 지탱하는 게임 수학 (0) | 2023.05.17 |




