cyphen156
게임 수학 12장-2 : 원근 투영(화면에 현실감을 부여하는 변환) - 깊이와 원근 보정 본문
이전 글에서 이어서 쓴다.
※ 여기서 설명하는 예제 순서는 책에서의 예제보다 1개 인덱스가 높습니다.
초점거리 왜곡과 깊이감
앞서 경험했던 렌더링 예제에서는 하나의 물체만을 그리고 있었기 때문에 별다른 문제를 발견하지 못했다.
하지만 사실 이건 컴퓨터 그래픽스에서 현실감과 몰입감을 방해하는 요소가 고려되어있지 않다.
바로 깊이감이다.
물체를 원근 투영 하여 그렸지만 사물이 화면에 그려지는 순서에 따라 먼저 그려진 그림이 덮어씌워져 나중에 그린 물체에 의해 가려져서 보인다. 예를 들자면 빨간 사각형을 그리고 그 위에 검은 원을 일부 겹쳐 그리는 듯하게 그린다는 것이다.
이러한 그리기 방식 때문에 물체가 가지고 있는 초점거리를 왜곡하는 현상이 발생한다.

절두체 :: 3차원 NDC
이제 이차원 평면 NDC를 깊이를 추가한 3차원 NDC공간으로 확장할 때가 되었다.
그러면 다음과 같이 모든 변의 길이가 2인 정육면체의 형태의 NDC공간이 탄생한다.

이러한 3차원 절두체 공간을 구현하기 위해 사각 뿔 형태인 사영 공간을 두개의 평면으로 자른다. 각각 근평면(Near Plane)과 원평면(Far Plane)이라 부른다. 그리고 이렇게 잘려진 사영공간은 사각 기둥의 형태를 띄게 되는데, 이를 절두체(Frustum)라고 부른다.
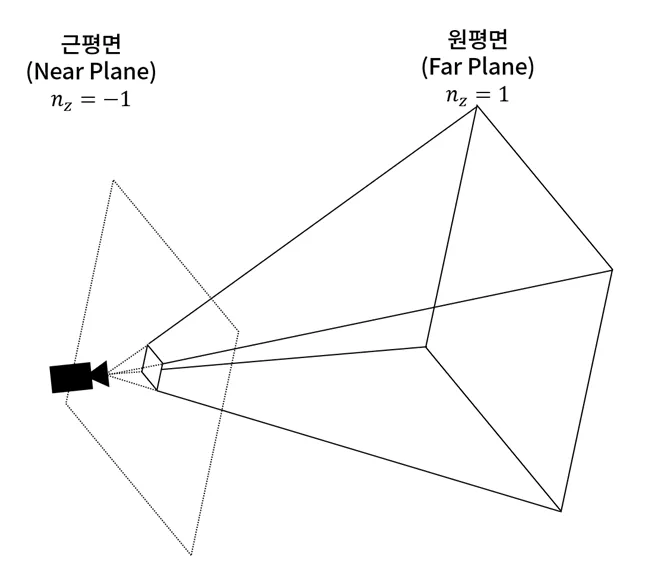
여기서 우리가 알 수 있는 것은 절두체 공간은 거리가 멀 수록 더 큰 깊이감을 갖기 때문에 왼손 좌표계를 통해 비교하면 더욱 공간 파악이 쉬워진 다는 것이다. 이제 까지 우리는 물체 기준으로 얼마나 가까이 있느냐를 판단했기 때문에 오른손 좌표계를 사용해왔지만 깊이감에 한해서는 왼손 좌표계 또한 고려할 때가 되었다.
2차원 좌표계에 사용되던 원근 투영 행렬은 3 * 3 행렬을 사용했었다. 그렇다면 3차원 절두체 공간에서는 4 * 4 행렬을 사용해야 한다는 소리가 된다. 그리고 이렇게 확장된 행렬에서 w값은 가상 차원수로 항상 고정되기때문에 마지막 행과 마지막 열의 요소에 사용되어야 한다. 그렇게 되면 남는 것은 4 * 4 행렬의 3행이 비게 되는데 이 행이 바로 절두체 공간에서 깊이감을 계산할 요소가 들어갈 행이 된다.
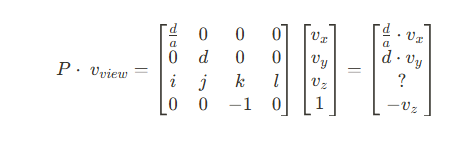
여기서 i, j는 x와 y의 요소에 대응되는데 깊이감과는 관계가 없어야 하기 때문에, 각각 외적연산시 평행한 요소가 발생시키고, 그 값은 항상 0이 된다. 따라서 i와 j는 연산의 편의를 위해 0이 되어야만 한다. 만약 그렇지 못하다면 깊이감에 왜곡을 줄 수 있다.
이제 남은것은 k와 l이다. 이 두 요소에 대응하는 값을 찾기 위해 두 개의 샘플을 절두체 공간에서 가져올 수 있다.
앞서 절두체 공간은 변이 2인 정육면체라고 하였다. 그렇다면 카메라로부터 절두체 원점을 지나는 직선을 그었을 때 정육면체와의 접점이 두개 생기는데 그 좌표의 거리가 2만큼 차이가 날 것이다.
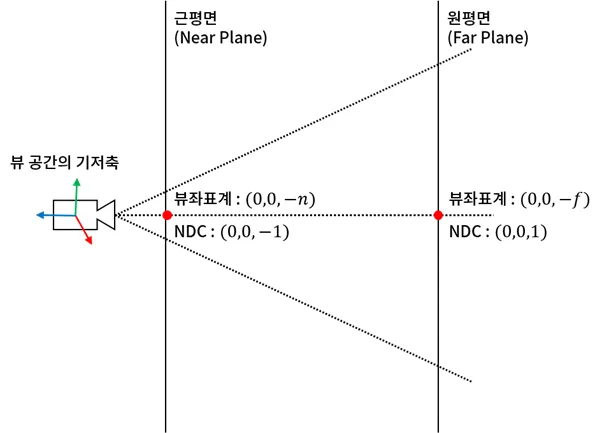
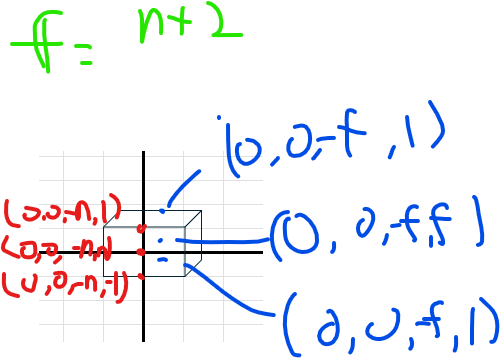
여기서 계산하기 쉽도록 두 행렬식을 구한다면 다음과 같은데 3행과 뷰 공간의 점을 내적하면 두개의 방정식을 얻을 수 있다.

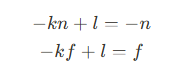
여기서 n과 f은 카메라에 설정되어 있는 상수이므로 두 식을 서로 빼 l을 소거한다면 K값을 구할 수 있다. 그리고 K값을 구했다면 L값 또한 구할 수 있다.
K = (f + n) / (f - n), L = -n(k+1) || f(k-1) == 2nf(n-f)
※ 주의해야 할 점은 위 그림에서 f = n+2라고 선언하였는데 이것은 정규화 절두 공간에서만 성립하는 수식이다.
실제 절두 공간은 카메라의 설정값에 따르므로 다음과 같이 변환 될 수 있다. n = 0.1f; f = 100.0f;
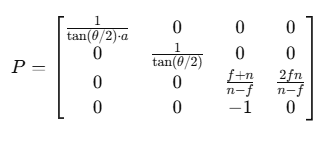
예제 12_3 깊이에 대한 정보 얻기
Engine/Public/3D/CameraObject.h
public:
FORCEINLINE Matrix4x4 GetPerspectiveViewMatrix() const;
private:
float _NearZ = 5.5f;
float _FarZ = 5000.f;
FORCEINLINE Matrix4x4 CameraObject::GetPerspectiveMatrix() const
{
float invA = 1.f / _ViewportSize.AspectRatio();
float d = 1.f / tanf(Math::Deg2Rad(_FOV) * 0.5f);
// 근평면과 원평면에 반대 부호를 붙여서 계산
float invNF = 1.f / (_NearZ - _FarZ);
float k = (_NearZ + _FarZ) * invNF;
float l = 2.f * _FarZ * _NearZ * invNF;
return Matrix4x4(
Vector4::UnitX * invA * d,
Vector4::UnitY * d,
Vector4(0.f, 0.f, k, -1.f),
Vector4(0.f, 0.f, l, 0.f)
);
}
FORCEINLINE Matrix4x4 CameraObject::GetPerspectiveViewMatrix() const
{
// 뷰 행렬 관련 요소
Vector3 viewX, viewY, viewZ;
GetViewAxes(viewX, viewY, viewZ);
Vector3 pos = _Transform.GetPosition();
float zPos = viewZ.Dot(pos);
// 투영 행렬 관련 요소
float invA = 1.f / _ViewportSize.AspectRatio();
float d = 1.f / tanf(Math::Deg2Rad(_FOV) * 0.5f);
float dx = invA * d;
float invNF = 1.f / (_NearZ - _FarZ);
float k = (_FarZ + _NearZ) * invNF;
float l = 2.f * _FarZ * _NearZ * invNF;
return Matrix4x4(
Vector4(dx * viewX.X, d * viewY.X, k * viewZ.X, -viewZ.X),
Vector4(dx * viewX.Y, d * viewY.Y, k * viewZ.Y, -viewZ.Y),
Vector4(dx * viewX.Z, d * viewY.Z, k * viewZ.Z, -viewZ.Z),
Vector4(-dx * viewX.Dot(pos), -d * viewY.Dot(pos), -k * zPos + l, zPos)
);
}SoftRenderer3D.cpp
Render3D()함수 수정내용
/// 예제 12_3 깊이에 대한 정보 얻기
const Matrix4x4 pvMatrix = mainCamera.GetPerspectiveViewMatrix();
for (auto it = g.SceneBegin(); it != g.SceneEnd(); ++it)
{
const GameObject& gameObject = *(*it);
if (!gameObject.HasMesh() || !gameObject.IsVisible())
{
continue;
}
// 렌더링에 필요한 게임 오브젝트의 주요 레퍼런스를 얻기
const Mesh& mesh = g.GetMesh(gameObject.GetMeshKey());
const TransformComponent& transform = gameObject.GetTransform();
Matrix4x4 finalMatrix = pMatrix * vMatrix * transform.GetModelingMatrix();
/// 예제 12_3 깊이에 대한 정보 얻기
Matrix4x4 finalMatrix2 = pvMatrix * transform.GetModelingMatrix();
// 메시 그리기
DrawMesh3D(mesh, finalMatrix, gameObject.GetColor());
DrawMesh3D(mesh, finalMatrix2, LinearColor::Red);
if (gameObject == PlayerGo)
{
// 플레이어 관련 정보
Vector4 clippedPos = pvMatrix * Vector4(transform.GetPosition());
float cameraDepth = clippedPos.W;
if (cameraDepth == 0) cameraDepth = SMALL_NUMBER;
float ndcZ = clippedPos.Z / cameraDepth;
r.PushStatisticText("Player: " + transform.GetPosition().ToString());
r.PushStatisticText("Depth: " + std::to_string(ndcZ));
r.PushStatisticText("Distance: " + std::to_string(clippedPos.W));
}
}원근 보정 매핑
이제 정상적으로 물체가 3차원 처럼 보이는지 확인해보자

책에서 보여주는 왜곡 문제이다. 어느 정도의 변화는 감안할 수 있지만 아예 눈썹 방향이 역전되어 캐릭터의 감정을 정 반대로 보여줄 정도로 왜곡이 심하다. 이걸 보정하는 방법이 필요하다. 이것은 사영공간의 무게중심 좌표와 NDC 절두체 공간의 무게중심 좌표가 서로 다르다는 것에서 나오는 문제점이다.
다음 화면은 실제로 렌더링 했을때 나타나는 문제점이다.
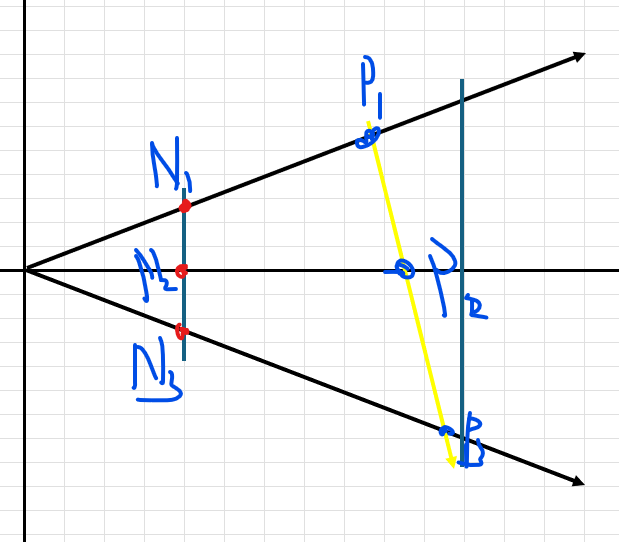
이러한 문제를 바로잡으려면 투영 과정을 거꾸로 추적해 NDC에서 구한 무게 중심 좌표로부터 사영 공간의 무게 중심 좌표를 계산하여 매핑해야 한다.
이러한 과정을 투영 보정 보간(Perspective Correction interPolation)이라 부른다.
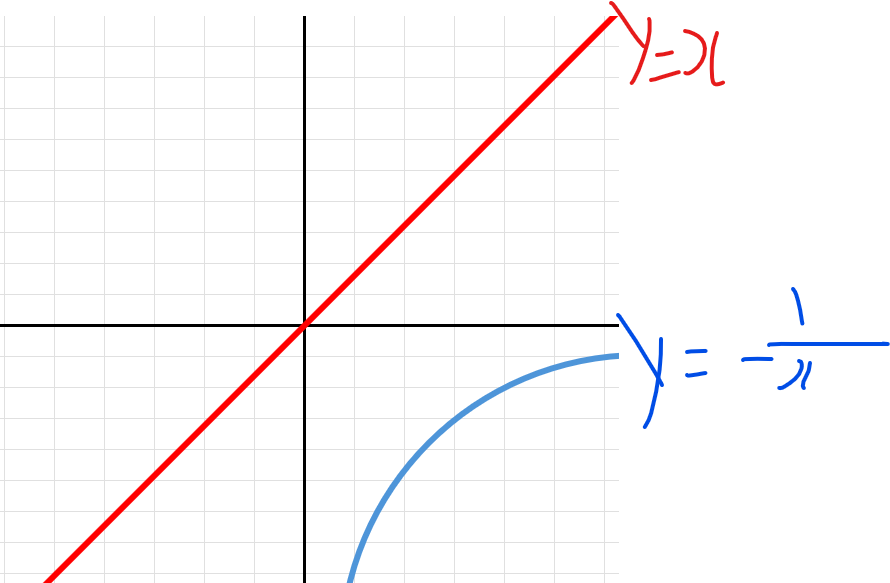
보통 우리가 사용하는 **선형 보간(Linear Interpolation)**은
두 점 A, B 사이의 값을 단순하게 t를 기준으로 보간하는 방식이다.
Lerp = (1 - t) * A + t * B하지만 이 방식은 원근 투영(Perspective Projection) 이후에는 정확하지 않다.
투영 변환은 z값에 따라 x, y, 속성 값들(예: UV, normal 등)까지 비선형적으로 왜곡되기 때문이다.
즉, z축 깊이에 따라 공간의 비율이 달라진다는 점을 무시하면 보간된 결과가 실제와 달라지게 된다.
대표적인 그래프가 y = 1 / -x 이다.
그런데 우리가 사용하는 공식은 보간식이므로 두 무게중심의 합 (NDC 무게 중심 + 사영 무게 중심)의 일반화 값은 1이 되어야 함을 알 수 있다.
정리하자면
우리가 사용하는 보간식은 무게 중심 좌표(Barycentric Coordinates) 기반이기 때문에, 어떤 방식으로든 보간 가중치들의 합은 항상 1이 되어야 한다.
이는 선형 보간은 물론, 투영 보정 보간에서도 마찬가지이며, 속성 값들을 보간하기 전, 각 정점 속성을 1/w로 정규화하여 보간한 뒤, 다시 전체 w로 나눠서 전체 무게 중심의 합이 1이 되도록 조정하게 된다.
결국, NDC 공간과 사영 공간의 무게 중심 좌표가 다르더라도, 이 보정 과정을 통해 우리가 얻고자 하는 정확한 보간 결과가 보장된다.
예제 12_4 찌그러진 캐릭터 얼굴을 올바로 잡기
GameEngine.cpp
LoadResources()함수 수정 내용
// 큐브 메시
Mesh& cubeMesh = CreateMesh(GameEngine::CubeMesh);
auto& v = cubeMesh.GetVertices();
auto& i = cubeMesh.GetIndices();
auto& uv = cubeMesh.GetUVs();
static const float halfSize = 0.5f;
std::transform(cubeMeshPositions.begin(), cubeMeshPositions.end(), std::back_inserter(v), [&](auto& p) { return p * halfSize; });
std::transform(cubeMeshIndice.begin(), cubeMeshIndice.end(), std::back_inserter(i), [&](auto& p) { return p; });
uv = {
// Right
Vector2(0.f, 48.f) / 64.f, Vector2(8.f, 48.f) / 64.f, Vector2(8.f, 56.f) / 64.f, Vector2(0.f, 56.f) / 64.f,
// Front
Vector2(8.f, 48.f) / 64.f, Vector2(8.f, 56.f) / 64.f, Vector2(16.f, 56.f) / 64.f, Vector2(16.f, 48.f) / 64.f,
// Back
Vector2(32.f, 48.f) / 64.f, Vector2(32.f, 56.f) / 64.f, Vector2(24.f, 56.f) / 64.f, Vector2(24.f, 48.f) / 64.f,
// Left
Vector2(24.f, 48.f) / 64.f, Vector2(16.f, 48.f) / 64.f, Vector2(16.f, 56.f) / 64.f, Vector2(24.f, 56.f) / 64.f,
// Top
Vector2(8.f, 64.f) / 64.f, Vector2(16.f, 64.f) / 64.f, Vector2(16.f, 56.f) / 64.f, Vector2(8.f, 56.f) / 64.f,
// Bottom
Vector2(16.f, 64.f) / 64.f, Vector2(24.f, 64.f) / 64.f, Vector2(24.f, 56.f) / 64.f, Vector2(16.f, 56.f) / 64.f
};SoftRenderer3D.cpp
DrawTringle3D()함수 수정내용
if (IsWireframeDrawing())
{
LinearColor finalColor = _WireframeColor;
if (InColor != LinearColor::Error)
{
finalColor = InColor;
}
r.DrawLine(InVertices[0].Position, InVertices[1].Position, finalColor);
r.DrawLine(InVertices[0].Position, InVertices[2].Position, finalColor);
r.DrawLine(InVertices[1].Position, InVertices[2].Position, finalColor);
}
else
{
const Texture& mainTexture = g.GetTexture(GameEngine::BaseTexture);
// 삼각형 칠하기
// 삼각형의 영역 설정
Vector2 minPos(Math::Min3(InVertices[0].Position.X, InVertices[1].Position.X, InVertices[2].Position.X), Math::Min3(InVertices[0].Position.Y, InVertices[1].Position.Y, InVertices[2].Position.Y));
Vector2 maxPos(Math::Max3(InVertices[0].Position.X, InVertices[1].Position.X, InVertices[2].Position.X), Math::Max3(InVertices[0].Position.Y, InVertices[1].Position.Y, InVertices[2].Position.Y));
// 무게중심좌표를 위해 점을 벡터로 변환
Vector2 u = InVertices[1].Position.ToVector2() - InVertices[0].Position.ToVector2();
Vector2 v = InVertices[2].Position.ToVector2() - InVertices[0].Position.ToVector2();
// 공통 분모 값 ( uu * vv - uv * uv )
float udotv = u.Dot(v);
float vdotv = v.Dot(v);
float udotu = u.Dot(u);
float denominator = udotv * udotv - vdotv * udotu;
// 퇴화 삼각형 판정.
if (denominator == 0.f)
{
return;
}
float invDenominator = 1.f / denominator;
ScreenPoint lowerLeftPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, minPos);
ScreenPoint upperRightPoint = ScreenPoint::ToScreenCoordinate(_ScreenSize, maxPos);
// 두 점이 화면 밖을 벗어나는 경우 클리핑 처리
lowerLeftPoint.X = Math::Max(0, lowerLeftPoint.X);
lowerLeftPoint.Y = Math::Min(_ScreenSize.Y, lowerLeftPoint.Y);
upperRightPoint.X = Math::Min(_ScreenSize.X, upperRightPoint.X);
upperRightPoint.Y = Math::Max(0, upperRightPoint.Y);
// 각 정점마다 보존된 뷰 공간의 z값
float invZ0 = 1.f / InVertices[0].Position.W;
float invZ1 = 1.f / InVertices[1].Position.W;
float invZ2 = 1.f / InVertices[2].Position.W;
// 삼각형 영역 내 모든 점을 점검하고 색칠
for (int x = lowerLeftPoint.X; x <= upperRightPoint.X; ++x)
{
for (int y = upperRightPoint.Y; y <= lowerLeftPoint.Y; ++y)
{
ScreenPoint fragment = ScreenPoint(x, y);
Vector2 pointToTest = fragment.ToCartesianCoordinate(_ScreenSize);
Vector2 w = pointToTest - InVertices[0].Position.ToVector2();
float wdotu = w.Dot(u);
float wdotv = w.Dot(v);
float s = (wdotv * udotv - wdotu * vdotv) * invDenominator;
float t = (wdotu * udotv - wdotv * udotu) * invDenominator;
float oneMinusST = 1.f - s - t;
if (((s >= 0.f) && (s <= 1.f)) && ((t >= 0.f) && (t <= 1.f)) && ((oneMinusST >= 0.f) && (oneMinusST <= 1.f)))
{
// 투영보정에 사용할 공통 분모
float z = invZ0 * oneMinusST + invZ1 * s + invZ2 * t;
float invZ = 1.f / z;
Vector2 targetUV = (InVertices[0].UV * oneMinusST * invZ0 + InVertices[1].UV * s * invZ1 + InVertices[2].UV * t * invZ2) * invZ;
r.DrawPoint(fragment, FragmentShader3D(mainTexture.GetSample(targetUV), LinearColor::White));
}
}
}
}만약 두 물체가 서로 비슷한 초점거리에 위치해서 겹쳐져 있다면 어떨까?
깊이 버퍼 활용하기
이제는 단순히 오브젝트 단위의 정렬이 아니라, 픽셀 단위로 정확하게 깊이를 계산해서 어느 픽셀이 화면상 앞에 있어야 하는지를 판단해야 한다. 그래야만 올바른 순서를 계산하고 정확하게 그려낼 수 있다.
이를 위해 매번 픽셀까지의 거리를 구하는 것이 아니라, 앞서 사용했던 정점 버퍼와 인덱스 버퍼의 역할을 하는 깊이 버퍼(Depth Buffer) 또는 Z-Buffer를 만들어서 물체에 대한 정보를 저장하는 것이다.
여기서 저장되는 물체의 정보는 월드 좌표계가 기준이 된다. 로컬 좌표계에서는 그 위치가 항상 변하기 때문에 사용 할 수 없기 때문이다.
깊이 버퍼를 사용하면 장점이 또 있다. 뒤에 있는 사물을 그려내지 않아도 되기 때문에 컬링의 효과를 갖을 수 있다.
예제 12_5 깊이 버퍼를 사용해 원근감 올바르게 표현하기
SoftRenderer3D.cpp
LoadScene3D()함수 수정 내용
/// 예제 12_5 깊이 버퍼를 사용해 원근감 올바르게 표현하기
constexpr float cubeScale = 100.f;
// 고정 시드로 랜덤하게 생성
std::mt19937 generator(0);
std::uniform_real_distribution<float> distZ(-1500.f, 0.f);
std::uniform_real_distribution<float> distXY(-1000.f, 1000.f);
// 100개의 큐브 오브젝트 생성하기
for (int i = 0; i < 100; ++i)
{
char name[64];
std::snprintf(name, sizeof(name), "GameObject%d", i);
GameObject& newGo = g.CreateNewGameObject(name);
newGo.GetTransform().SetPosition(Vector3(distXY(generator), distXY(generator), distZ(generator)));
newGo.GetTransform().SetScale(Vector3::One * cubeScale);
newGo.SetMesh(GameEngine::CubeMesh);
}전역 변수 수정 내용
// 실습 설정을 위한 변수
/// 예제 12_5 깊이 버퍼를 사용해 원근감 올바르게 표현하기
bool toggleDepthTesting = true;Update3D()함수 수정 내용
/// 예제 12_5 깊이 버퍼를 사용해 원근감 올바르게 표현하기
if (input.IsReleased(InputButton::Space))
{
toggleDepthTesting = !toggleDepthTesting;
}이제 여기에 삼각형에서 깊이 버퍼를 통해 테스팅을 수행하자
DrawTringle3D()함수 수정내용
/// 예제 12_5 깊이 버퍼를 사용해 원근감 올바르게 표현하기
if (toggleDepthTesting)
{
float newDepth = InVertices[0].Position.Z * oneMinusST + InVertices[1].Position.Z * s + InVertices[2].Position.Z * t;
float prevDepth = r.GetDepthBufferValue(fragment);
if (newDepth < prevDepth)
{
// 픽셀 처리 전 깊이 값을 버퍼에 보관
r.SetDepthBufferValue(fragment, newDepth);
}
else
{ // 앞에 뭐가 있으면 그리지 않ㄱ;
continue;
}
}예제 12_6 깊이 버퍼 시각화하기
Engine/Public/3D/CameraObject.h
public:
/// 예제 12_6 깊이 버퍼 시각화하기
float GetNearZ() const { return _NearZ; }
float GetFarZ() const { return _FarZ; }SoftRenderer3D.cpp
전역 변수 수정 내용
/// 예제 12_6 깊이 버퍼 시각화하기
bool useLinearVisualization = true;Update3D() 함수 수정 내용
if (input.IsReleased(InputButton::Z))
{
/// 예제 12_6 깊이 버퍼 시각화하기
useLinearVisualization = !useLinearVisualization;
}DrawTringle3D()함수 수정내용
/// 예제 12_6 깊이 버퍼 시각화하기
const CameraObject& mainCamera = g.GetMainCamera();
// 카메라의 근평면과 원평면값
float n = mainCamera.GetNearZ();
float f = mainCamera.GetFarZ();
/*------------------------------------*/
/// 예제 12_2 변경된 삼각형을 그리는 로직
// 클립 좌표를 NDC좌표로 변경
//for (auto& v : InVertices)
//{
// // 무한 원점인 경우, 약간 보정해준다.
// // 카메라랑 겹치면 안되니까
// if (v.Position.Z == 0.f)
// {
// v.Position.Z = SMALL_NUMBER;
// }
// float invZ = 1.f / v.Position.Z;
// v.Position.X *= invZ;
// v.Position.Y *= invZ;
// v.Position.Z *= invZ;
//}
/// 예제 12_6 깊이 버퍼 시각화하기
for (auto& v : InVertices)
{
// 무한 원점인 경우, 약간 보정해준다.
// 카메라랑 겹치면 안되니까
if (v.Position.W == 0.f)
{
v.Position.W = SMALL_NUMBER;
}
float invW = 1.f / v.Position.W;
v.Position.X *= invW;
v.Position.Y *= invW;
v.Position.Z *= invW;
}
/*------------------------------------*/
/// 예제 12_6 깊이 버퍼 시각화하기
if (IsDepthBufferDrawing())
{
if (useLinearVisualization)
{
// 카메라로부터의 거리에 따라 균일하게 증감하는 흑백 값으로 변환
grayScale = (invZ - n) / (f - n);
}
// 뎁스 버퍼 그리기
r.DrawPoint(fragment, LinearColor::White * grayScale);
}
이제 다 끝난것 같지만 이런 미친상황이 나온다....
아직도 해야할게 남아있나...
죽여줘....
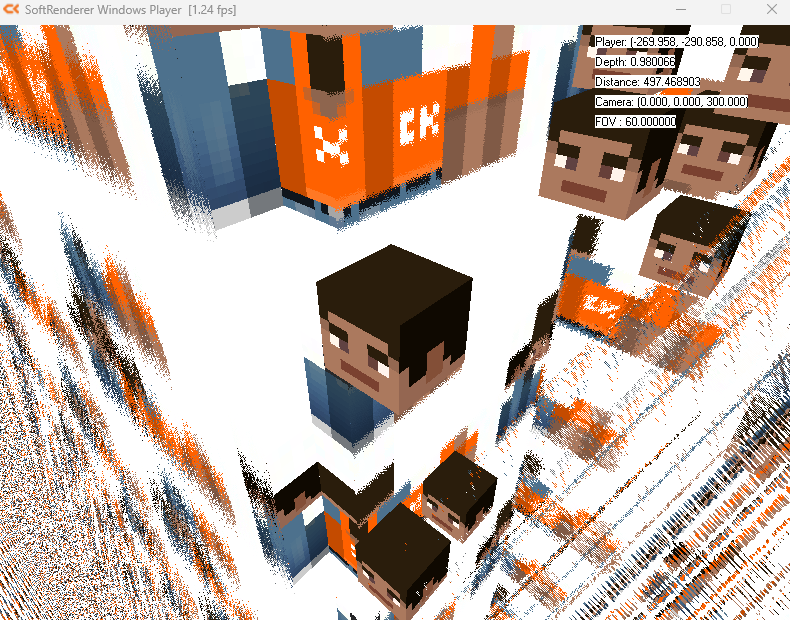
이것은 사영공간 구조로 인해 발생하는 문제로서 13장에서 다룬다고 한다. 절두체를 통해 최적화 된 공간을 만들어보자!
모든 예제 코드의 소스파일은
GitHub - onlybooks/gamemath: <이득우의 게임 수학> 공식 깃허브 페이지
GitHub - onlybooks/gamemath: <이득우의 게임 수학> 공식 깃허브 페이지
<이득우의 게임 수학> 공식 깃허브 페이지. Contribute to onlybooks/gamemath development by creating an account on GitHub.
github.com
또한 제 개인 깃허브 레포지토리 에 있습니다.
Workspace/C++/GameMath at main · cyphen156/Workspace · GitHub
Workspace/C++/GameMath at main · cyphen156/Workspace
Studying . Contribute to cyphen156/Workspace development by creating an account on GitHub.
github.com
=※ 이득우 교수님의 인프런 게임수학강의를 참고하여 작성되었습니다.
흠;;;;;12장 하는데 3일 걸렷는데;;;? 2일안에 5장 마무리 할수 잇나....?
토요일은 일가야되는데...????????
흠;;;;;;;;;;;;
'수학 > 게임수학' 카테고리의 다른 글
| 게임 수학 12장-1 : 원근 투영(화면에 현실감을 부여하는 변환) - 원근투영과 동차좌표 (0) | 2025.04.04 |
|---|---|
| 게임 수학 11장 : 외적(3차원 공간의 분석과 응용) (1) | 2025.04.02 |
| 게임 수학 10장 : 3차원 공간(입체 공간의 생성)-3차원 트랜스폼과 오일러각 (1) | 2025.03.24 |
| 게임 수학 9장 : 게임 엔진(콘텐츠를 만드는 기술) (3) | 2025.03.21 |
| 게임 수학 8장 : 삼각형(물체를 구성하는 가장 작은 단위)-메시와 텍스쳐 (0) | 2025.03.19 |





