cyphen156
게임 수학 12장-1 : 원근 투영(화면에 현실감을 부여하는 변환) - 원근투영과 동차좌표 본문
모니터는 항상 2차원 평면이기 때문에, 현실 세계처럼 입체감 있는 그림을 그리는 것은 매우 어렵습니다. 그래서 2차원 이미지를 3차원처럼 보이게 만드는 기법이 중요한데, 이를 원근 투영(Perspective Projection)이라고 부른다.
이러한 원근감 표현은 르네상스 시대에도 이미 존재했으며, 한 점을 기준으로 직선 거리를 설정하고, 거리에 따라 같은 사물이라도 비율을 다르게 그리는 방식이 고안되었고, 현대에 이르러서는 이 '한 점'을 카메라와 같은 물체의 시점으로 일반화하여 세상을 바라보게 되었다. 이를 화각(Field of View, FOV)이라고 부릅니다.
원근 투영은 기존의 직교 투영 방식에서 한 점으로 모이기 때문에 뷰 모델이 6면체의 형태에서 사각 뿔의 형태로 변화하게 된다. 모든 물체는 하나의 평면 위에 존재할 수 있고, 이 평면들을 다시 모니터에 포개어 하나로 합쳐 표현한다면 2차원 공간에 3차원 공간을 표현할 수 있게 되는데 이것을 투영 평면(Projection Plane)이라고 부른다.
원근 투영에서는 3차원 공간의 모든 물체가 카메라의 시점을 기준으로 하나의 투영 평면에 사영된다. 이때 각 물체는 고유한 z값(깊이)을 가지고 있지만, 사영 결과는 모두 동일한 투영 평면 위에 맺힌다. 이런 관점에서 보면, 투영 평면은 깊이가 다른 여러 사영 평면의 결과가 모인 하나의 표현 공간이라 할 수 있다.
카메라로부터 투영 평면 까지의 거리를 초점거리(Focal Length)라고 부른다.

원근 투영을 구하기 위해서는 우선 투영평면의 위치를 지정하고, 이 투영 평면에 대응하는 2차원 평면의 좌표 시스템을 만들어야 하는데, 이것을 NDC(Normalized device coordinate)라고 부른다.
NDC
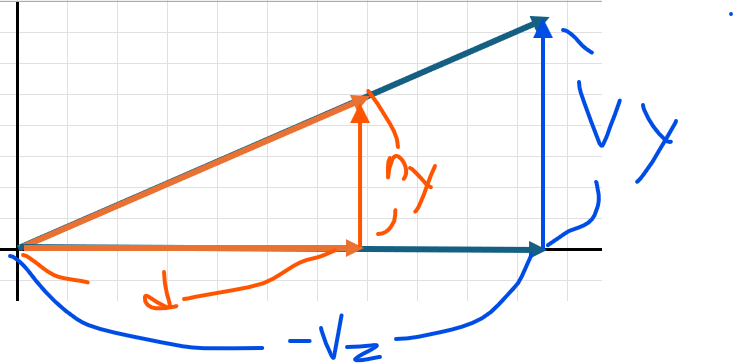
투영 평면에 대응하는 NDC는 언제나 일정한 값을 가져야 한다면 카메라에 설정된 화각에 따라 초점 거리가 달라질 수 밖에 없다. 화각이 커질수록 초점 거리가 가까워지고, 화각이 작아질 수록 초점 거리는 멀어진다.
뭔가 또 생각난다....
맞다 이번에도 삼각함수다.
초점거리는 화각에 따라 Tan함수에 영향을 받는다.
focalLength = 1 / tan(fov / 2)초점거리를 구했다면, 이제 남은 일은 3D 뷰 공간의 점을 2D 투영 평면 위의 점으로 대응시키는 변환 행렬, 즉 원근 투영 행렬을 설계해야 한다.
이 행렬은 단순히 x, y, z를 비례로 줄이는 것이 아니라, z값에 따라 x와 y를 나눠서 비율을 조절해야 하는 특징을 갖는다.
유클리드 공간과의 차이
우리가 지금까지 다뤄온 모든 공간 변환(T, R, S)은 공통적으로 다음과 같은 특성을 가졌습니다:
- 각 축이 서로 직교하고,
- 각 축의 단위 길이가 동일하며,
- 3차원 공간이 정육면체처럼 균일한 구조로 구성됨
이러한 공간을 유클리드 공간(Euclidean Space)이라고 부르며, 이에 기반한 기하학을 유클리드 기하학이라고 한다.
하지만 원근 투영은 이와 다르다.
원근 투영에서는 z축(깊이)에 따라 x, y 좌표의 비율이 달라지기 때문에, 결과적으로는 기존의 유클리드 공간에서 비유클리드적 공간으로 옮겨간다 즉, 투영 변환은 단순한 공간 변환이 아닌 '공간의 해석 방식 자체를 바꾸는 변환'이다.
사영공간
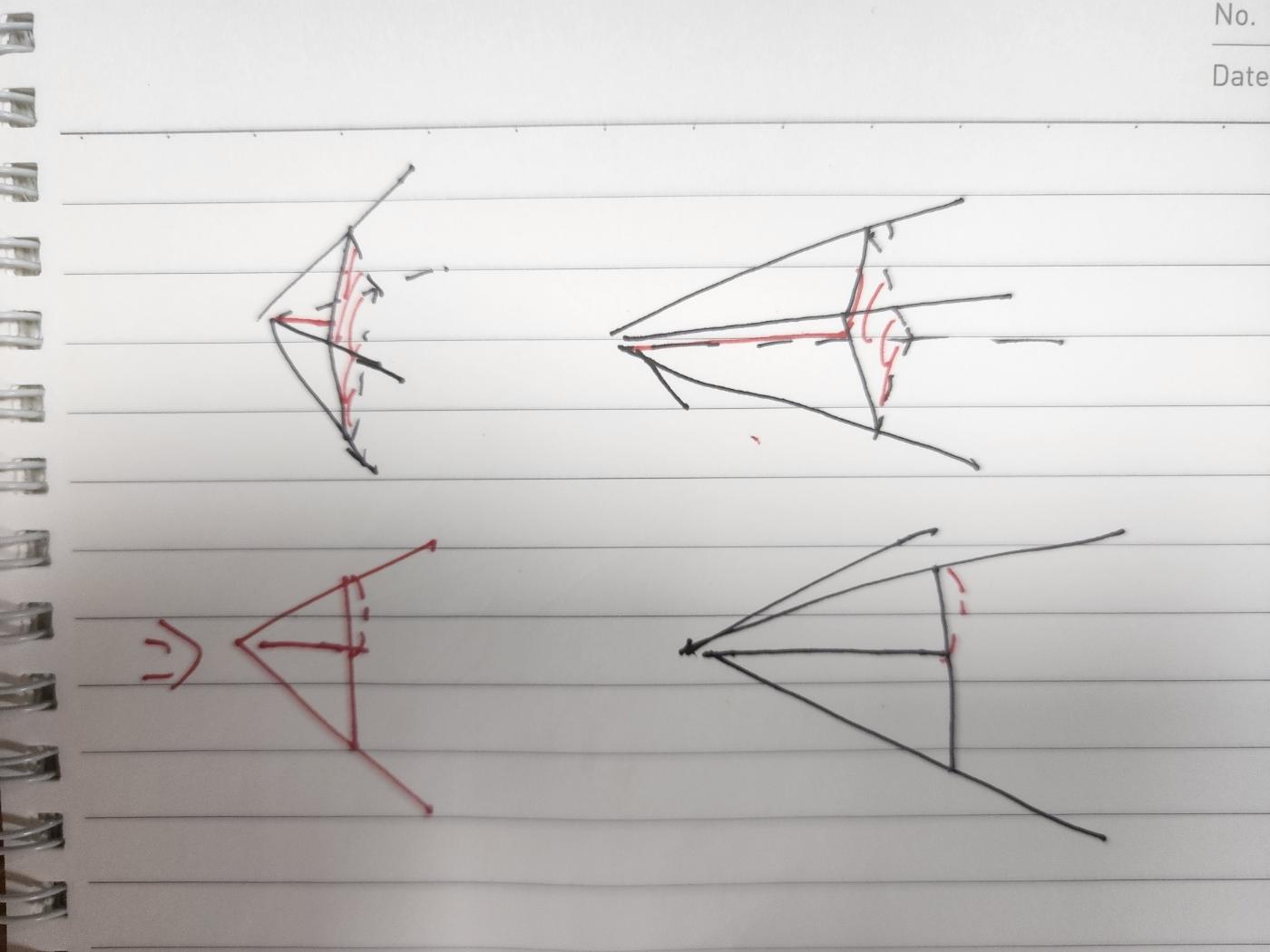
앞서 원근 투영시 뷰 공간을 사각 뿔의 형태로 바라보게 된다고 언급하였는데, 이 사각 뿔의 영역을 사영 공간이라고 부른다.
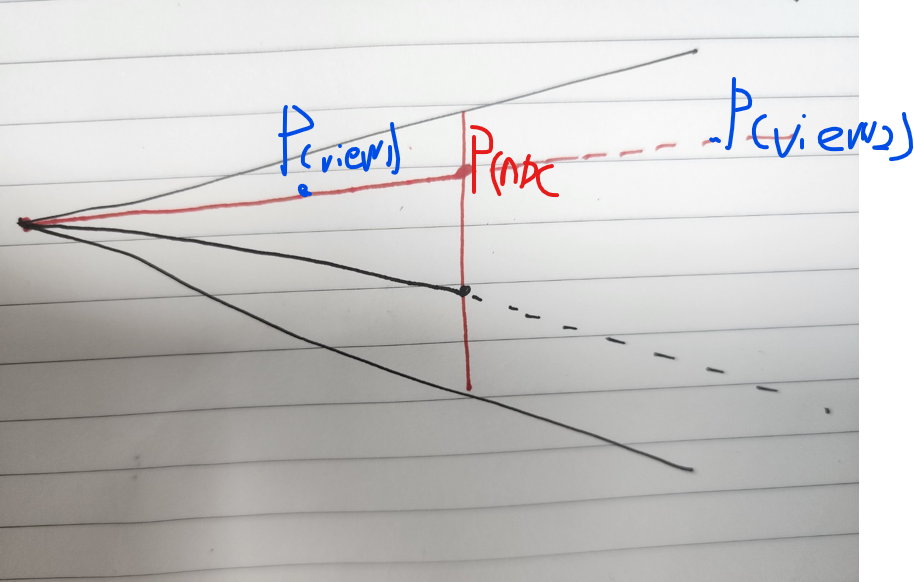
위 그림을 보면 삼각형의 닮음 비를 이용하여 원래의 위치에서 NDC의 좌표를 구할 수 있다.
d : Ny = Vy : -Vz여기서 Ny의 값은 (D * Vy) / -Vz로 구할 수 있고, 카메라의 좌우와 상하 시야각은 동일하므로, Nx = Ny라 볼 수 있다.
따라서 P(ndc)의 좌표는 D / -Vz(Vx, Vy)가 된다.
그런데 이것으로 끝내서는 안된다.
우리가 현실에서 사용하는 모니터들은 모두 종횡비와 해상도가 다르다. (21 : 9, 18 : 9 / 1920 | 1080, 720 | 480등)
이와 같은 모니터의 특성을 고려하지 않는다면 다음과 같이 그림이 일그러져 화면에 출력된다.
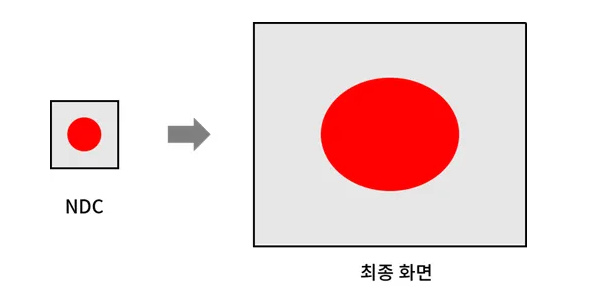
해결하는 방법은 간단하다.
모니터의 해상도를 거꾸로 투영 행렬에 적용(역행렬)하면 된다.
그런데 아직 문제가 남아있다. 행렬 연산은 파이프 라인을 통해 연산량을 줄이기 위해 사용하는 것인데, 모든 물체마다 Vz값이 다르므로, 카메라에 비치는 물체의 갯수 만큼 연산량이 늘어난다.
그래서 투영 행렬에서 분모인 -Vz값을 제거(클립 공간)하고, 결과에 -Vz를 나눠준다면 해결된다.
이렇게 생성된 벡터는 원래 얻어야 했던 NDC 좌표와는 다르지만 원근투영행렬 P는 물체까지의 -Vz와는 무관하게 카메라 설정 값으로만 구성되는 보편적 행렬식이 되고, 이 행렬연산의 결과에 -Vz를 나눠주면 된다.
Perspective Divide는 사실상, 원래 행렬 곱의 모든 요소에 분산되어 있던 -Vz 나눗셈을 벡터 결과에 대한 스칼라 곱 형태로 통합한 것이다.
이를 통해 우리는 정점마다 개별 좌표마다 반복되는 나눗셈을 피하고, 하나의 스칼라 연산으로 원근 투영 결과를 얻게 된다.
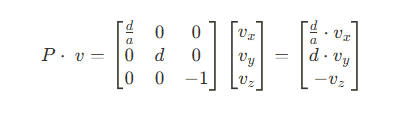
동차 좌표계
위에서 원근 투영행렬을 구했지만 한가지 문제가 발생했다. 모든 물체에 대한 투영행렬 연산의 결과에 -Vz를 나눈 것이 아직 신뢰할만 하다는 것을 증명하지 못했다는 것이다. 앞서 -Vz의 길이는 모든 물체가 서로 다를 수 있다고 했다. 그러면 행렬 연산의 결과에 -Vz를 나눠주는것도 결국 투영된 물체의 갯수만큼 반복해야 하는것 아닌가?
이에 대한 해답이 동차 좌표계에 존재한다.
동차 좌표계에서는 모든 항의 차수가 같음을 의미하는데, 한단계 상위 차원의 수(W)를 사용하여 모든 차원의 항을 마지막 차원 항으로 나눈 값이었다고 가정하는 것이다.
어떤 벡터 (x, y, z, w)는 사실상 정규화된 벡터 (x/w, y/w, z/w, 1)와 동일한 점을 의미한다고 가정하고, 마지막에 w를 다시 곱함으로써 (x, y, z, w)가 도출된다.
즉, 차원이 높은 공간에서의 점은, 최종적으로 w로 나눈 결과만이 의미를 가지며, 이 w는 우리가 원하는 정규화된 "실공간상의" 좌표로 되돌리는 기준이 된다.
- 3D 좌표 (x, y, z)를 → 4D 좌표 (x, y, z, 1)로 확장하고,
- 투영 행렬 연산 결과는 (x', y', z', w') 형태로 나오며,
- 마지막에 w'로 전체 벡터를 나눠주는 퍼스펙티브 디바이드를 수행합니다.
이렇게 하면 -Vz에 대한 연산은 벡터 하나당 한 번만 수행하면 되고, x, y, z 모두에 자동으로 반영된다.
※ 주저리주저리 또 써놨는데 핵심은 마지막 가상 차원 벡터 요소(W)를 -Vz라 가정하고 이것을 기준으로 정규화 한다면 다른 모든요소 (X, Y, Z)들은 다시 반정규화를 진행했을 때 항상 같은 차수(1)을 갖게 된다는 것을 의미한다. ※
다음은 GPT가 정리해준 동차 좌표계의 내용이다.
🧠 동차 좌표계와 원근 투영의 수학적 정당성
앞에서 원근 투영 행렬을 통해 정점 (x, y, z)에 대해
투영 좌표 (x', y') = (f * x / -z, f * y / -z)를 계산했습니다.
하지만 여기에는 한 가지 근본적인 문제가 남아 있습니다.
❗ 문제 제기
모든 물체는 서로 다른 z값(Vz)을 갖기 때문에,
결국 행렬 연산 결과에 -Vz를 나눠줘야 하는데,
그렇다면 정점마다 나눗셈이 반복되어야 하는 것 아닌가?
정점 수만큼 나눗셈을 반복한다면 과연 이게 최적화된 방식인가?
그리고 이렇게 해도 우리가 원하는 투영 결과가 정확히 나오긴 할까?
💡 해답은 동차 좌표계(Homogeneous Coordinates)에 있다
🔷 동차 좌표계의 철학
동차 좌표계는 기본적으로 다음과 같은 가정을 전제로 합니다:
어떤 벡터 (x, y, z, w)는
정규화된 벡터 (x/w, y/w, z/w, 1)과 동일한 위치를 가진다.
즉, 실제 공간상의 좌표는 (x/w, y/w, z/w)이고,
벡터 (x, y, z, w)는 단지 그것을 표현하기 위한 확장 표현일 뿐이라는 거죠.
📌 중요한 해석
**"모든 항의 차수가 같다"**는 건
결국 우리가 (x/w, y/w, z/w)처럼 모든 항에 동일한 분모(w)를 적용하고,
다시 그 w를 곱하면 항의 차수가 모두 1로 통일된다는 뜻입니다.
즉, 차원이 높은 공간에서의 점은, 그 자체로 의미가 있는 게 아니라,
정규화된 형태만이 ‘실공간상의 의미’를 가지는 것이고,
그 정규화의 기준이 되는 값이 바로 w = -Vz인 것입니다.
🧮 직관적으로 다시 요약
- (x, y, z, 1) × P → (x', y', z', w')
- 이때 w' = -Vz, 그 외는 z에 대한 비례 항
- x_ndc = x' / w', y_ndc = y' / w', z_ndc = z' / w'
- → 이 결과는 **(f * x / -z, f * y / -z, z')**로 우리가 원한 결과와 일치
✅ 결론
퍼스펙티브 디바이드는 단순히 "나중에 나눠준다"는 수준이 아니다.
이는 동차 좌표계의 정의, 즉 **"모든 항은 마지막 항으로 나눈 결과만이 의미를 가진다"**는 철학에 기반한다.그리고 w = -Vz로 설계된 원근 투영 행렬은
정점마다 다른 z값을 갖더라도,
동차 좌표계 상에서 단 하나의 스칼라 w로 정규화가 가능하게 설계되었기 때문에,
우리는 정점마다 반복되는 나눗셈 없이도
수학적으로 완전한 결과를 보장받을 수 있다.
결국 핵심은, 마지막 가상 차원 벡터 요소 w = -Vz를 기준으로 정규화하면
다른 모든 요소 (x, y, z)는 다시 반정규화를 해도 차수 1을 유지하게 된다는 점이다.이것이 바로 동차 좌표계가 원근 투영을 처리할 수 있는 수학적, 구조적 이유다.
예제 12_1 원근 투영 행렬을 적용한 렌더링 로직
SoftRenderer3D.cpp
Update3D()함수 수정내용
/// 예제 12_1 원근 투영 행렬을 적용한 렌더링 로직
// 12_1 로컬 변수
static float fovSpeed = 100.f;
static float minFov = 15.f;
static float maxFov = 150.f;
// 12_1 카메라 트랜스폼
float deltaFov = input.GetAxis(InputAxis::WAxis) * fovSpeed * InDeltaSeconds;
camera.SetFOV(Math::Clamp(camera.GetFOV() + deltaFov, minFov, maxFov));Render3D()함수 수정내용
/// 예제 12_1 원근 투영 행렬을 적용한 렌더링 로직
const Matrix4x4 pMatrix = mainCamera.GetPerspectiveMatrix();
for (auto it = g.SceneBegin(); it != g.SceneEnd(); ++it)
{
const GameObject& gameObject = *(*it);
if (!gameObject.HasMesh() || !gameObject.IsVisible())
{
continue;
}
// 렌더링에 필요한 게임 오브젝트의 주요 레퍼런스를 얻기
const Mesh& mesh = g.GetMesh(gameObject.GetMeshKey());
const TransformComponent& transform = gameObject.GetTransform();
Matrix4x4 finalMatrix = pMatrix * vMatrix * transform.GetModelingMatrix();
예제 12_2 변경된 삼각형을 그리는 로직
SoftRenderer3D.cpp
DrawTriangle3D()함수 수정내용
/// 예제 12_1 원근 투영 행렬을 적용한 렌더링 로직
// 12_1 로컬 변수
static float fovSpeed = 100.f;
static float minFov = 15.f;
static float maxFov = 150.f;
// 12_1 카메라 트랜스폼
float deltaFov = input.GetAxis(InputAxis::WAxis) * fovSpeed * InDeltaSeconds;
camera.SetFOV(Math::Clamp(camera.GetFOV() + deltaFov, minFov, maxFov));Render3D()함수 수정내용
/// 예제 12_1 원근 투영 행렬을 적용한 렌더링 로직
const Matrix4x4 pMatrix = mainCamera.GetPerspectiveMatrix();
for (auto it = g.SceneBegin(); it != g.SceneEnd(); ++it)
{
const GameObject& gameObject = *(*it);
if (!gameObject.HasMesh() || !gameObject.IsVisible())
{
continue;
}
// 렌더링에 필요한 게임 오브젝트의 주요 레퍼런스를 얻기
const Mesh& mesh = g.GetMesh(gameObject.GetMeshKey());
const TransformComponent& transform = gameObject.GetTransform();
Matrix4x4 finalMatrix = pMatrix * vMatrix * transform.GetModelingMatrix();모든 예제 코드의 소스파일은
GitHub - onlybooks/gamemath: <이득우의 게임 수학> 공식 깃허브 페이지
GitHub - onlybooks/gamemath: <이득우의 게임 수학> 공식 깃허브 페이지
<이득우의 게임 수학> 공식 깃허브 페이지. Contribute to onlybooks/gamemath development by creating an account on GitHub.
github.com
또한 제 개인 깃허브 레포지토리 에 있습니다.
Workspace/C++/GameMath at main · cyphen156/Workspace · GitHub
Workspace/C++/GameMath at main · cyphen156/Workspace
Studying . Contribute to cyphen156/Workspace development by creating an account on GitHub.
github.com
※ 이득우 교수님의 인프런 게임수학강의를 참고하여 작성되었습니다.
'수학 > 게임수학' 카테고리의 다른 글
| 게임 수학 12장-2 : 원근 투영(화면에 현실감을 부여하는 변환) - 깊이와 원근 보정 (2) | 2025.04.04 |
|---|---|
| 게임 수학 11장 : 외적(3차원 공간의 분석과 응용) (1) | 2025.04.02 |
| 게임 수학 10장 : 3차원 공간(입체 공간의 생성)-3차원 트랜스폼과 오일러각 (1) | 2025.03.24 |
| 게임 수학 9장 : 게임 엔진(콘텐츠를 만드는 기술) (3) | 2025.03.21 |
| 게임 수학 8장 : 삼각형(물체를 구성하는 가장 작은 단위)-메시와 텍스쳐 (0) | 2025.03.19 |





