| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- Noam Nisan
- Shimon Schocken
- JavaScript
- 생능출판
- 이득우
- 잡생각 정리글
- booksr.co.kr
- BOJ
- (주)책만
- 데이터 통신과 컴퓨터 네트워크
- 김진홍 옮김
- 밑바닥부터 만드는 컴퓨팅 시스템 2판
- 주우석
- 백준
- The Elements of Computing Systems 2/E
- 전공자를 위한 C언어 프로그래밍
- C#
- 이득우의 게임수학
- 일기
- C++
- 메타버스
- C
- HANBIT Academy
- unity6
- 입출력과 사칙연산
- 게임 수학
- hanbit.co.kr
- https://insightbook.co.kr/
- 박기현
- 알고리즘
- Today
- Total
cyphen156
알고리듬 # 5 정렬과 재귀 본문
수열과 정렬의 차이
수열은 단순히 수나 데이터를 순서대로 나열한 것이다.
정렬은 단순히 나열된 상태를 넘어, 특정 기준(오름차순, 내림차순, 사전식 등) 에 맞춰 데이터를 배열하는 과정을 말한다.
정렬의 중요성
- 데이터 위치 파악 용이
데이터가 어떤 기준으로 정리되어 있으면 원하는 값을 쉽게 찾을 수 있습니다. - 탐색 속도 향상
정렬된 데이터에서는 이진 탐색(Binary Search) 같은 효율적인 탐색 알고리즘을 적용할 수 있어, 단순 순차 탐색(O(N))보다 훨씬 빠른 O(log N) 시간 안에 원하는 값을 찾을 수 있게 해준다.- 검색에 사용된 알고리듬에 따라, 데이터가 저장된 구조에 따라 자료의 검색 시간이 획기적으로 차이가 나게 된다.
- 다른 알고리의 기반
정렬은 그 자체로도 중요하지만, 이후 다른 알고리즘(탐색, 최적화, 데이터 압축, 중복 제거 등)의 전제 조건으로 자주 사용된다.
1. 평범한 정렬 방법
일반적으로 가장 구현하기 쉬운, 시간복잡도가 O(N²)인 정렬 알고리즘이다.
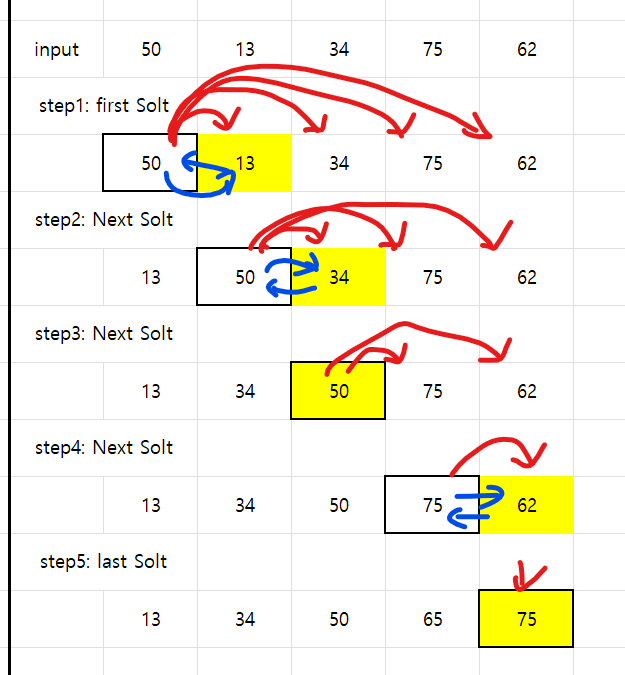
선택 정렬(Selection Sort)
N개의 자료에 대해서 매 번 1개의 데이터 선택하여 다른 N개의 데이터와 비교해가며 정렬을 수행하기 때문에 선택 정렬이라 부른다.
여기서 한가지의 최적화 힌트는
1. 이미 정렬된 데이터는 비교 연산을 수행하지 않고(현재 슬롯보다 앞의 자료)
2. 자기 자신은 비교해봣자 같다는 것이 나올 테니 자기 다음부터만 비교하는 것이고
3. 마지막 스텝에서는 데이터가 자기 자신밖에 존재하지 않기 때문에 비교를 수행하지 않는 것이다.
그래서 실질적으로 O(N^2)보다는 덜 걸리지만 빅-오 표기법에 의해 시간복잡도는 O(N^2)그대로 표현된다.
알고리듬/5. 정렬과 재귀/선택정렬.c
단순히 배열과 사이즈를 입력받아서 정렬을 오름차순 정렬을 수행한다.
내림차순 정렬의 경우 비교 방향만 바꿔주면 된다.
#include <stdio.h>
void SelectionSort(int arr[], int size)
{
for (int i = 0; i < size - 1; ++i)
{
int min_idx = i;
for (int j = i + 1; j < size; ++j)
{
if (arr[j] < arr[min_idx])
{
min_idx = j;
}
}
if (min_idx != i)
{
int t = arr[i];
arr[i] = arr[min_idx];
arr[min_idx] = t;
}
}
}버블 정렬(Bubble sort)
버블 정렬의 경우 선택 정렬과 다르게 최대나 최소 값을 맨 마지막 요소로 밀어내면서 인접한 두 요소끼리만을 비교한다.
그렇기 때문에 아래 그림처럼 하늘색칸인 두 요소끼리만 비교하면서 마지막에 보라색으로 확정된다.
만약 한 번의 사이클에서 교환이 한 번도 일어나지 않으면, 이미 정렬된 상태이므로 조기 종료 최적화가 가능하다.
그래서 시간복잡도가 최선의 경우 O(N), 최악의 경우 O(N²)일 수 있다.

알고리듬/5. 정렬과 재귀/버블정렬.c
#include <stdio.h>
#include <stdbool.h>
void BubbleSort(int arr[], int size)
{
for (int i = 0; i < size - 1; ++i)
{
bool isSwapped = false;
for (int j = 0; j < size - i - 1; ++j)
{
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
isSwapped = true;
}
}
if (!isSwapped)
{
break;
}
}
}삽입 정렬(Insertion sort)
삽입 정렬의 경우 특정 위치에 데이터를 끼워 넣는 동작을 수행하는 정렬이다.
배열을 정렬된 구간과 정렬되지 않은 구간으로 나누어 생각한다.
정렬되지 않은 구간에서 원소 하나(key)를 꺼내어, 정렬된 구간 안에서 올바른 위치를 찾아 삽입한다.
삽입 정렬의 경우 시간복잡도가 이미 정렬된 데이터일 경우 최선O(N), 하나도 정렬되지 않은 경우 최악 O(N²)으로 버블 소트와 비슷하다.
그럼에도 불구하고 삽입정렬이 버블 정렬보다 효과적인 이유는 스왑 연산 발생 횟수가 더 적기 때문이다.
동작 원리
- 첫 번째 요소는 이미 정렬된 것으로 간주한다.
- 두 번째 요소부터 시작하여, 선택된 요소(key)를 왼쪽의 정렬된 구간과 비교한다.
- key보다 큰 값들은 한 칸씩 뒤로 이동시킨다.
- 빈 자리에 key를 삽입한다.
- 이 과정을 배열 끝까지 반복하면 전체가 정렬된다.

알고리듬/5. 정렬과 재귀/삽입정렬.c
#include <stdio.h>
void InsertionSort(int arr[], int size)
{
for (int i = 1; i < size; ++i)
{
int key = arr[i];
int j;
// 뒤에서 앞으로 탐색하면서 이동
for (j = i - 1; j >= 0; --j)
{
if (arr[j] > key)
{
arr[j + 1] = arr[j]; // 한 칸 뒤로 밀기
}
else
{
break; // 자기 자리를 찾으면 종료
}
}
arr[j + 1] = key; // key 삽입
}
}재귀(Recursive)
재귀는 함수가 자기 자신을 반복적으로 호출하여 문제를 푸는 방법이다.
반복문과 동일한 표현력을 가지며 코드가 간결해질 수 있지만,
호출 스택 비용과 과도한 재귀 깊이에 따른 스택 오버플로우 위험이 있다.
그렇기 때문에 반드시 기저 조건(base case) 을 두어 함수 호출을 종료해야 한다.
기저 조건을 잘못 설정하면 무한 호출로 스택 오버플로우가 발생한다.
필자의 경우 재귀 호출보다는 단일 함수에서 모두 처리하는 것을 선호하는 편이다.
우선 재귀 호출의 경우 기저 조건 비교연산이 필수이기 때문에
필연적으로 연산시간이 느려지기도 하고,
흐름이 눈에 명확하게 보이지 않는 경우가 많기 때문이다.
대표적으로 재귀 함수를 사용하는 예시는 팩토리얼(N!)연산과, 분할 정복이다.
재귀가 필수적인 경우가 있다.
바로 문제를 작은 단위로 쪼개어 해결하려 할 때이다.
이것을 분할 - 정복(Divide & Conquer) 기법이라 부른다.
분할 - 정복(Divide & Conquer)
분할 정복(Divide & Conquer)은 큰 문제를 작은 문제로 나누어 재귀적으로 해결하고,
그 결과를 합쳐 전체 문제를 해결하는 기법이다.
이 과정에서 작은 단위로 쪼개기 때문에 추가 메모리가 필요한 경우가 많다.
다만, 분할된 하위 문제들이 서로 독립적이지 않고 중복 계산이 많이 발생하는 경우가 있다.
이때는 중간 결과를 저장하는 메모이제이션(Memoization) 기법을 사용하여 불필요한 계산을 피할 수 있다.
이러한 접근을 일반화한 것이 동적 계획법(Dynamic Programming)으로, 분할 정복과 밀접한 관계를 가진다.
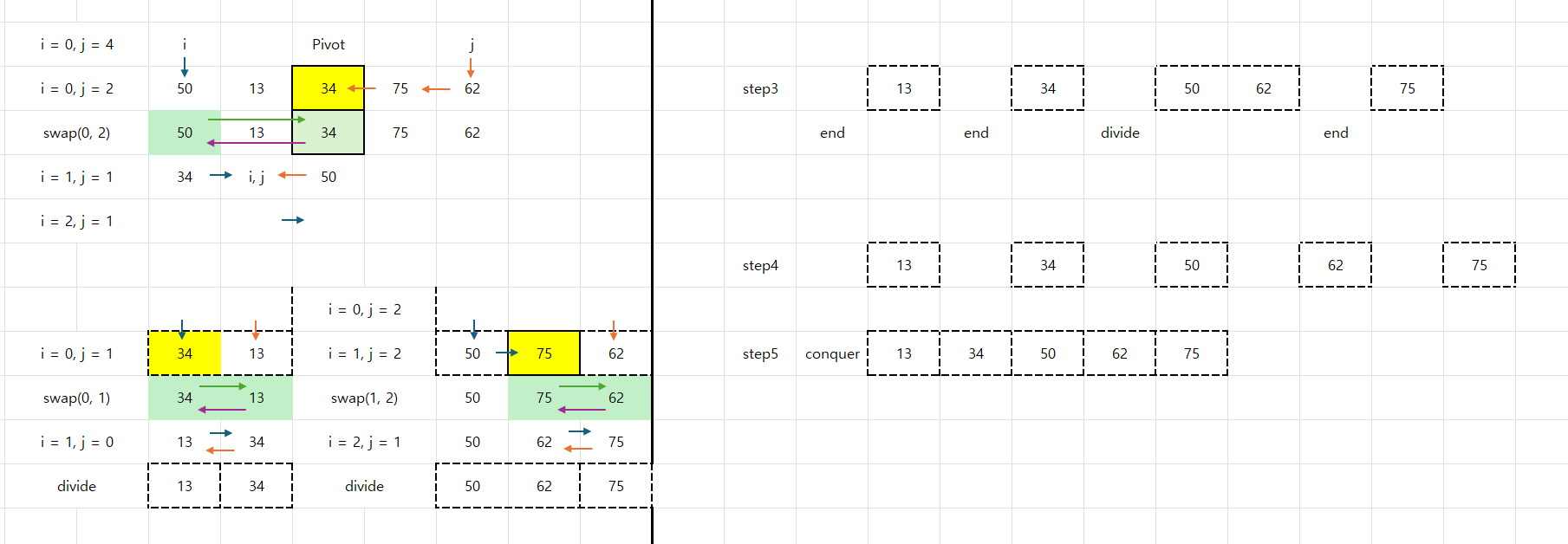
퀵 정렬(Quick Sort)
피벗을 기준으로 좌/우 분할 → 재귀 정렬
시간 복잡도: 평균 O(N log N), 최악 O(N²)
특징: 제자리(in-place) 정렬 가능, 불안정 정렬
알고리듬/5. 정렬과 재귀/퀵정렬.c
#include <stdbool.h>
void QuickSort(int arr[], int left, int right)
{
if (left >= right)
{
return;
}
int pivot = arr[left + (right - left) / 2];
int i = left; // l ptr
int j = right; // r ptr
while (true)
{
// 피벗보다 작은건 무시
while (i <= j && arr[i] < pivot)
{
++i;
}
// 피벗보다 큰거는 무시
while (i <= j && arr[j] > pivot)
{
--j;
}
// 만약 둘의 left index와 right index 크기 비교가 역전되면
// 이미 분할되어 있다는 소리
// 고로 반으로 쪼개서 그 안에서 재분할
if (i > j)
{
break;
}
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
++i;
--j;
}
QuickSort(arr, left, j);
QuickSort(arr, i, right);
}계수 정렬(Counting Sort)
값 자체를 인덱스로 사용하여 빈도를 증가시키는 방식
비교 기반 정렬이 아니기 때문에 O(N+K)라는 시간 복잡도를 가지고 있다.
시간 복잡도 : O(N + K) (원소 개수 + 데이터 값의 범위)
필자의 경우 특수 계수 정렬을 사용한다.
동적 자료 구조가 아닌 정적 자료를 사용한다면 공간 낭비가 심해지지만 자료의 삽입, 탐색시 시간이 O(1)로 줄어든다.
다만 삽입된 자료의 "순서"가 필요해질 경우 자료구조가 변해야 하며, 추가 알고리듬이 필요하여 탐색 시간이 O(N+K)라 된다.
알고리듬/5. 정렬과 재귀/계수정렬.c
#include <string.h>
#include <stdlib.h>
#define MAX_VALUE 0x7fffffff
void CountingSort(int arr[], int size)
{
int* count = (int*)malloc((MAX_VALUE + 1) * sizeof(int));
int* output = (int*)malloc(size * sizeof(int));
if (count == NULL || output == NULL)
{
if (count != NULL)
{
free(count);
}
if (output != NULL)
{
free(output);
}
return;
}
memset(count, 0, (MAX_VALUE + 1) * sizeof(int));
for (int i = 0; i < size; i++)
{
count[arr[i]]++;
}
for (int i = 1; i <= MAX_VALUE; i++)
{
count[i] += count[i - 1];
}
for (int i = size - 1; i >= 0; i--)
{
output[count[arr[i]] - 1] = arr[i];
count[arr[i]]--;
}
for (int i = 0; i < size; i++)
{
arr[i] = output[i];
}
free(count);
free(output);
}알고리듬/5. 정렬과 재귀/계수정렬_2.c
#define MAX_SIZE 0x7fffffff
int arr[MAX_SIZE] = { 0 };
void Insert(int data)
{
arr[data]++;
}
int Search(int data)
{
return arr[data];
}
int Order(int data)
{
int result = 0;
for (int i = 0; i <= data; ++i)
{
result += arr[i];
}
return result;
}병합 정렬(Merge Sort)
아이디어: 배열을 절반으로 분할 → 각각 정렬 → 두 정렬된 배열을 병합.
시간 복잡도: 항상 O(N log N)
특징: 안정 정렬, 추가 메모리 O(N) 필요
필자가 가장 좋아하는 정렬방법이다.

알고리듬/5. 정렬과 재귀/병합정렬.c
#include <stdlib.h>
void Merge(int arr[], int left, int right, int mid)
{
int lSize = mid - left + 1;
int rSize = right - mid;
int* lArr = (int*)malloc((lSize) * sizeof(int));
int* rArr = (int*)malloc((rSize) * sizeof(int));
if (lArr == NULL || rArr == NULL)
{
if (lArr != NULL)
{
free(lArr);
}
if (rArr != NULL)
{
free(rArr);
}
return;
}
for (int i = 0; i < lSize; ++i)
{
lArr[i] = arr[left + i];
}
for (int i = 0; i < rSize; ++i)
{
rArr[i] = arr[mid + 1 + i];
}
int i = 0;
int j = 0;
int k = left;
// 두 쪽 모두 남아있는 동안 병합
while (i < lSize && j < rSize)
{
if (lArr[i] <= rArr[j])
{
arr[k] = lArr[i];
i++;
}
else
{
arr[k] = rArr[j];
j++;
}
k++;
}
while (i < lSize)
{
arr[k] = lArr[i];
i++;
k++;
}
while (j < rSize)
{
arr[k] = rArr[j];
j++;
k++;
}
free(lArr);
free(rArr);
}
void MergeSort(int arr[], int left, int right)
{
// size <= 2
if (left >= right)
{
return;
}
int mid = left + (right - left) / 2;
MergeSort(arr, left, mid);
MergeSort(arr, mid + 1, right);
Merge(arr, left, right, mid);
}추가 예시 그림

다음 글에서는 분할 정복 기법에서 더 나아가 동적 계획법에 대해 설명하도록한다.
코테까지 10일쯤 남았는데 충분히 정리됬으면 좋겟다.
해당 코드들은 제 깃허브에 있습니다. 유사코드는 제공하지 않습니다.
Workspace/알고리듬 at main · cyphen156/Workspace
Workspace/알고리듬 at main · cyphen156/Workspace
Studying . Contribute to cyphen156/Workspace development by creating an account on GitHub.
github.com
'컴퓨터공학 > 알고리듬' 카테고리의 다른 글
| 알고리듬 #7 계산 기하학 : 컴퓨터로 그림 그려서 문제 풀기 (0) | 2025.09.12 |
|---|---|
| 알고리듬 #6 점화식과 동적계획법 : 규칙 찾아내기 (0) | 2025.09.11 |
| 알고리즘 #4 통계적 접근 : 확률과 기댓값 그리고 몬테카를로의 방법 (1) | 2025.09.04 |
| 알고리듬#3 경우의 수 : 순열과 조합 (0) | 2025.06.10 |
| 알고리듬#2 소수판정법(primarity Test) (1) | 2024.02.19 |




