| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- hanbit.co.kr
- unity6
- 이득우의 게임수학
- C#
- 알고리즘
- 일기
- BOJ
- 입출력과 사칙연산
- 주우석
- (주)책만
- 잡생각 정리글
- 김진홍 옮김
- C++
- C
- 데이터 통신과 컴퓨터 네트워크
- booksr.co.kr
- 백준
- Noam Nisan
- JavaScript
- 메타버스
- The Elements of Computing Systems 2/E
- https://insightbook.co.kr/
- Shimon Schocken
- 전공자를 위한 C언어 프로그래밍
- HANBIT Academy
- 밑바닥부터 만드는 컴퓨팅 시스템 2판
- 박기현
- 게임 수학
- 이득우
- 생능출판
- Today
- Total
cyphen156
알고리듬 #7 계산 기하학 : 컴퓨터로 그림 그려서 문제 풀기 본문
이번 챕터에서는 계산 기하학에 대해서 탐구한다.
대충 게임 수학때 햇던 내용을 떠올린다면 좋지 않을까? 싶다
'수학/게임수학' 카테고리의 글 목록
Cyphen의 개인 공부 블로그입니다. 프사는 아는 동생이 그려준 그림 주인장과 싱크로율 0%
cyphen156.tistory.com
이 책에서는 벡터의 내적과 외적에 대해서 간단하게 다루고 있고, 수식만 보여주자면 다음과 같다
벡터의 내적(Dot Product)과 외적(Cross Product)
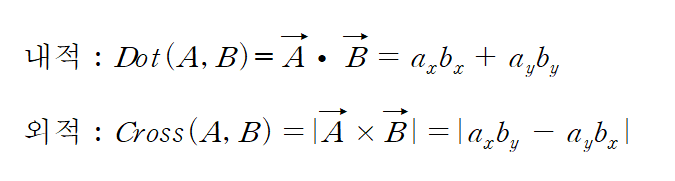
점과 선분의 거리 구하기
세 점을이 존재할 때 한 점과 다른 한 점을 이어 선분을 만들고, 마지막 남은 한 점과 선분 사이의 거리가 최소가 되는 길이(수선의 발의 길이)를 구하는 문제이다.
그림으로 표현하면 다음과 같이 표현된다.

그런데 사실 이것은 평행사변형의 높이와 같다.

또한 두 벡터의 외적의 결과는 평행사변형의 넓이와 같다.
따라서 두 벡터의 외적 결과에 한 벡터(밑변)를 나눠준다면 수선의 발을 구할 수 있다는 소리다.


알고리듬/7. 계산기하학/점과 선분의 거리.c
#include <stdio.h>
#include <math.h>
typedef struct Point
{
int x;
int y;
}Point;
typedef struct Vector
{
int x;
int y;
}Vector;
Vector CreateVectorFromPoints(Point A, Point B)
{
Vector v;
v.x = B.x - A.x;
v.y = B.y - A.y;
return v;
}
double Dot(Vector a, Vector b)
{
return a.x * b.x + a.y * b.y;
}
double Cross(Vector a, Vector b)
{
return a.x * b.y - a.y * b.x;
}
double Length(Vector v) {
return sqrt((double)v.x * v.x + (double)v.y * v.y);
}
int main(void)
{
Point A = {3, 5}, B = {5, 4}, C = {-3, 2};
Vector CA = CreateVectorFromPoints(C, A);
Vector CB = CreateVectorFromPoints(C, B);
printf("CA = (%d, %d)\n", CA.x, CA.y);
printf("CB = (%d, %d)\n", CB.x, CB.y);
double square = fabs(Cross(CB, CA));
double dist = square / Length(CB);
printf("From CB To A = %.5f\n", dist);
return 0;
}이것을 응용한 문제는 다양하지만 대표적인 기하 문제는 다음과 같다.
이중 최근접 점쌍 문제만 풀이해보도록 하겠다.
나머지 알고리즘은 어려워서 나중에 추가 글로 발행하기로 한다.
- 가장 가까운 점 찾기(최근접 점 쌍 문제)
- 볼록 다각형 만들기(Convex hull 구하기)
- 보르노이 다이어그램(Fortune 알고리듬)
- 미술관 문제
가장 가까운 점 찾기
N개의 점이 주어졌을 때 가장 가까운 두 점 사이의 거리를 구하는 문제
Naive 하게 푼다면 모든 점을 각각 벡터를 구성하면서 거리를 비교하므로, 시간복잡도는 O(N^2)이 걸린다.


분할 정복 기법을 사용한다면 O(N log N)으로 풀 수 있다.


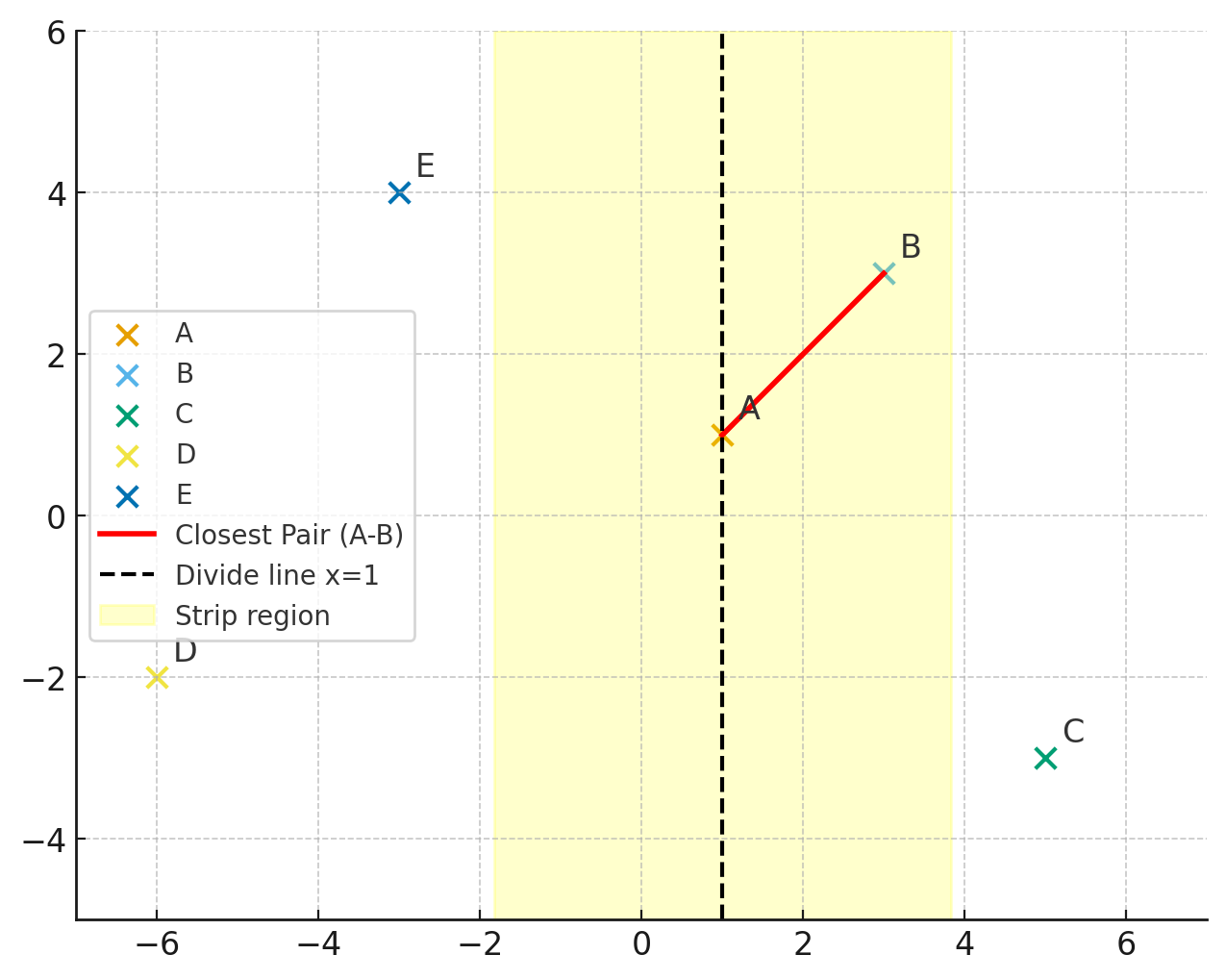
간단하게 분할 한번으로 시각화 하면 다음과 같다.
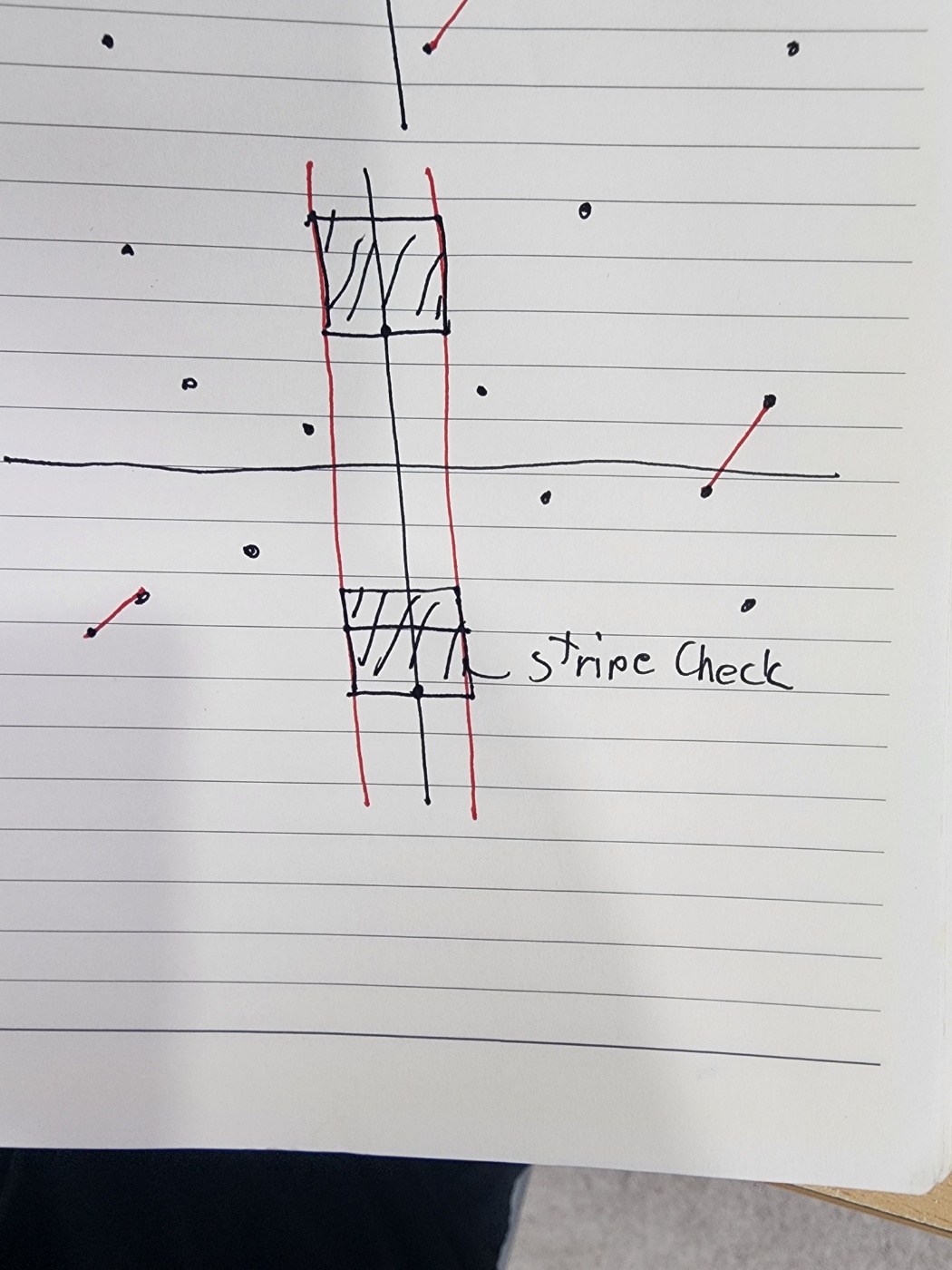
핵심 아이디어는 다음과 같다.
2차원 좌표인 점들을 한 축을 기준으로 정렬한다.
전체를 비교하지 않고 가운데 좌표를 기준으로 좌, 우를 배열의 요소가 2~3개가 남을 때까지 반복하여 분할한다.
분할이 완료 되었다면 요소 사이의 최소 거리를 구한다.
구해진 거리를 기준으로 stripe 범위를 형성하여 분할 축에 대해 y좌표를 올려가면서 최소 거리(d)를 갱신한다.
보통 계산 할 때는 한 좌표를 기준으로 6~7개 정도면 충분하다. 그 이상의 비교는 d보다 길어지기 때문이다.
이 과정을 병합해 가면서 마지막까지 구한다.
알고리듬/7. 계산기하학/가장 가까운 점 찾기.c
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
typedef struct Point
{
int x;
int y;
}Point;
int cmp_x(const void* p, const void* q)
{
const Point *a = (const Point*)p, *b = (const Point*)q;
if (a->x != b->x)
{
return (a->x < b->x) ? -1 : 1;
}
return (a->y < b->y) ? -1 : 1;
}
int cmp_y(const void* p, const void* q)
{
const Point *a = (const Point*)p, *b = (const Point*)q;
if (a->y != b->y)
{
return (a->y < b->y) ? -1 : 1;
}
return (a->x < b->x) ? -1 : 1;
}
double Distance(Point a, Point b)
{
return sqrt((double)(a.x - b.x) * (a.x - b.x) +
(double)(a.y - b.y) * (a.y - b.y));
}
double Solve(Point* px, int l, int r)
{
double best = 1e18;
for (int i = l; i < r; i++)
{
for (int j = i + 1; j < r; j++)
{
double d = Distance(px[i], px[j]);
if (d < best)
{
best = d;
}
}
}
return best;
}
double Stripe(Point* strip, int sz, double d)
{
double best = d;
qsort(strip, sz, sizeof(Point), cmp_y);
for (int i = 0; i < sz; i++)
{
for (int j = i + 1; j < sz; j++)
{
if (fabs((double)strip[j].y - (double)strip[i].y) >= best)
{
break;
}
double cur = Distance(strip[i], strip[j]);
if (cur < best)
{
best = cur;
}
}
}
return best;
}
double Divide(Point* px, Point* tmp, int l, int r)
{
int n = r - l;
if (n <= 3)
{
return Solve(px, l, r);
}
int m = l + n / 2;
int midx = px[m].x;
double dL = Divide(px, tmp, l, m);
double dR = Divide(px, tmp, m, r);
double d = (dL < dR) ? dL : dR;
int sz = 0;
for (int i = l; i < r; i++)
{
if (fabs((double)px[i].x - (double)midx) < d)
{
tmp[sz++] = px[i];
}
}
d = Stripe(tmp, sz, d);
return d;
}
int main(void)
{
int N;
scanf("%d", &N);
Point* points = malloc(N * sizeof(Point));
Point* tmp = malloc(N * sizeof(Point));
for (int i = 0; i < N; i++)
{
scanf("%d %d", &points[i].x, &points[i].y);
}
qsort(points, N, sizeof(Point), cmp_x);
double best2 = Divide(points, tmp, 0, N);
printf("%.6f\n", (best2));
free(tmp);
free(points);
return 0;
}해당 코드들은 제 깃허브에 있습니다. 유사코드는 제공하지 않습니다.
Workspace/알고리듬 at main · cyphen156/Workspace
Workspace/알고리듬 at main · cyphen156/Workspace
Studying . Contribute to cyphen156/Workspace development by creating an account on GitHub.
github.com
'컴퓨터공학 > 알고리듬' 카테고리의 다른 글
| 알고리듬 #9 뉴턴법과 근사해 : 미분·적분으로 수치 계산해보기 (0) | 2025.09.16 |
|---|---|
| 알고리듬 #8 누적합과 계차 : 효과적으로 수열 다루기 (0) | 2025.09.12 |
| 알고리듬 #6 점화식과 동적계획법 : 규칙 찾아내기 (0) | 2025.09.11 |
| 알고리듬 # 5 정렬과 재귀 (0) | 2025.09.11 |
| 알고리즘 #4 통계적 접근 : 확률과 기댓값 그리고 몬테카를로의 방법 (1) | 2025.09.04 |




