| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- JavaScript
- unity6
- (주)책만
- 박기현
- C
- 메타버스
- HANBIT Academy
- 이득우의 게임수학
- 일기
- 백준
- BOJ
- 전공자를 위한 C언어 프로그래밍
- 알고리즘
- 데이터 통신과 컴퓨터 네트워크
- 생능출판
- Noam Nisan
- 입출력과 사칙연산
- C++
- 밑바닥부터 만드는 컴퓨팅 시스템 2판
- 이득우
- The Elements of Computing Systems 2/E
- hanbit.co.kr
- C#
- Shimon Schocken
- 잡생각 정리글
- 주우석
- https://insightbook.co.kr/
- booksr.co.kr
- 김진홍 옮김
- 게임 수학
- Today
- Total
cyphen156
알고리듬 #8 누적합과 계차 : 효과적으로 수열 다루기 본문
이번 글에서는 누적합과 계차라는 서로 반대 개념을 다룬다.
이 둘을 다루기 전에 먼저 구간합에 대해 알아야 한다.
구간합이란?
수열이 있을 때 특정 구간(Chunk , Segment)단위로 요소들의 합을 빠르게 구하는 것이다.
예: A=[2,4,5,1,3]A = [2, 4, 5, 1, 3] 일 때,
- 구간합(2~4번 원소) = A[2]+A[3]+A[4]=4+5+1=10A[2] + A[3] + A[4] = 4 + 5 + 1 = 10.
- 단순하게 구하면 O(N), 질의가 많아지면 비효율적.
→ 이를 빠르게 하기 위해 누적합을 사용한다.
누적합(Prefix Sum)
S[i]=A[1]+A[2]+⋯+A[i]
누적합은 수열의 요소들을 처음부터 자기 자신까지를 미리 더해놓고, 이를 기록해 놓았다가 구간합을 구할 때 누적합 끼리 빼면 특정 구간의 합만을 빠르게 구할 수 있다는 점에서 착안한 기법이다.
대표적인 Memoization을 활용한 전처리 기법이며, DP에서 자주 응용된다
수식으로 표현하자면
A[l..r]=S[r]−S[l−1]
가 되기 때문에 O(1)로 연산이 가능하다.
알고리듬/8. 누적합과 계차/누적합.c
long long prefix_sum(long long* A, int size, long long* S)
{
S[0] = 0;
for (int i = 1; i <= size; i++)
{
S[i] = S[i - 1] + A[i];
}
return 0;
}알고리듬/8. 누적합과 계차/구간합.c
#include "누적합.c"
long long SectorSum(long long* S, int start, int end)
{
return S[end] - S[start - 1];
}
long long SectorSum_Naive(long long* A, int start, int end)
{
long long result = 0;
for (int i = start; i <= end; ++i)
{
result += A[i];
}
return result;
}계차(Difference Array)
D[1]=A[1],D[i]=A[i]−A[i−1](i>1)
인접 원소의 차이를 기록한 배열
누적합과는 다르게 구간을 빠르게 갱신하는 것에 초점을 맞춘다.
누적합이 구간합을 구할때는 빠르지만, 누적합을 구성하는 시간 자체는 O(n)이기 때문에 원본 배열의 요소에 수정이 많을 경우 매우 비효율적이게 된다.
때문에 구간 업데이트를 빠르게 하기 위해 계차를 두고, 최종적으로 누적합으로 복원한다.
알고리듬/8. 누적합과 계차/계차.c
void build_diff(long long* A, int N, long long* D)
{
D[1] = A[1];
for (int i = 2; i <= N; i++)
{
D[i] = A[i] - A[i - 1];
}
D[N + 1] = 0; // 가드
}
void range_add(long long* D, int l, int r, long long v)
{
D[l] += v;
D[r + 1] -= v;
}
void restore_from_diff(long long* D, int N, long long* A)
{
A[1] = D[1];
for (int i = 2; i <= N; i++)
{
A[i] = A[i - 1] + D[i];
}
}업데이트도 많고, 중간중간 바로 구간합 질의도 많다면 (온라인 처리)
→ Fenwick 트리(BIT) / 세그먼트 트리(지연 전파) 로 모두 O(logN) 에 처리하는 것이 표준.
- 오프라인(업데이트 몰아서, 마지막에만 결과): 계차 + 누적합
- 온라인(업데이트/질의 섞임): BIT/세그먼트 트리
이중 세그먼트 트리에 대해서 배운다.
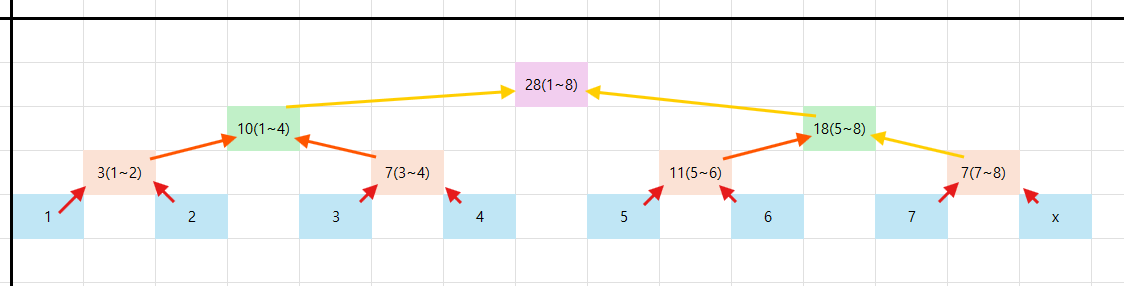
세그먼트 트리(Segment Tree)
배열 구간의 정보를 완전 이진 트리 형태로 관리하는 자료구조
시간복잡도
- 빌드(build): O(N)
- 질의(query): O(log N)
- 갱신(update): O(log N)
특징
- 리프 노드는 원본 배열에 해당한다.
- 부모 노드는 구간합에 해당한다.
따라서 부모-자식 관계를 이용하여 구간합을 빠르게 구할 수 있다.
알고리듬/8. 누적합과 계차/세그먼트 트리.c
#include <stdio.h>
#include <stdlib.h>
void build(long long* tree, long long* A, int node, int start, int end)
{
if (start == end)
{
tree[node] = A[start];
}
else
{
int mid = (start + end) / 2;
build(tree, A, node * 2, start, mid);
build(tree, A, node * 2 + 1, mid + 1, end);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
}
void push(long long* tree, long long* lazy, int node, int start, int end)
{
if (lazy[node] != 0)
{
long long add = lazy[node];
tree[node] += add * (end - start + 1);
if (start != end)
{
lazy[node * 2] += add;
lazy[node * 2 + 1] += add;
}
lazy[node] = 0;
}
}
void update_range_add(long long* tree, long long* lazy,
int node, int start, int end, int l, int r, long long val)
{
push(tree, lazy, node, start, end);
if (r < start || end < l)
{
return;
}
if (l <= start && end <= r)
{
lazy[node] += val;
push(tree, lazy, node, start, end);
return;
}
int mid = (start + end) / 2;
update_range_add(tree, lazy, node * 2, start, mid, l, r, val);
update_range_add(tree, lazy, node * 2 + 1, mid + 1, end, l, r, val);
tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
long long query_range_sum(long long* tree, long long* lazy,
int node, int start, int end, int l, int r)
{
push(tree, lazy, node, start, end);
if (r < start || end < l)
{
return 0;
}
if (l <= start && end <= r)
{
return tree[node];
}
int mid = (start + end) / 2;
long long L = query_range_sum(tree, lazy, node * 2, start, mid, l, r);
long long R = query_range_sum(tree, lazy, node * 2 + 1, mid + 1, end, l, r);
return L + R;
}Workspace/알고리듬 at main · cyphen156/Workspace
Workspace/알고리듬 at main · cyphen156/Workspace
Studying . Contribute to cyphen156/Workspace development by creating an account on GitHub.
github.com
'컴퓨터공학 > 알고리듬' 카테고리의 다른 글
| 알고리듬 Extra #1 최단경로 구하기 : 다익스트라를 일부만 정렬해서 최단거리 구하기 (0) | 2025.09.17 |
|---|---|
| 알고리듬 #9 뉴턴법과 근사해 : 미분·적분으로 수치 계산해보기 (0) | 2025.09.16 |
| 알고리듬 #7 계산 기하학 : 컴퓨터로 그림 그려서 문제 풀기 (0) | 2025.09.12 |
| 알고리듬 #6 점화식과 동적계획법 : 규칙 찾아내기 (0) | 2025.09.11 |
| 알고리듬 # 5 정렬과 재귀 (0) | 2025.09.11 |




