| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- https://insightbook.co.kr/
- 박기현
- 밑바닥부터 만드는 컴퓨팅 시스템 2판
- 이득우
- 일기
- 알고리즘
- booksr.co.kr
- 데이터 통신과 컴퓨터 네트워크
- 백준
- C
- 이득우의 게임수학
- C#
- hanbit.co.kr
- 김진홍 옮김
- Noam Nisan
- The Elements of Computing Systems 2/E
- JavaScript
- 잡생각 정리글
- 게임 수학
- 메타버스
- 생능출판
- 입출력과 사칙연산
- unity6
- (주)책만
- HANBIT Academy
- 전공자를 위한 C언어 프로그래밍
- BOJ
- Shimon Schocken
- 주우석
- C++
Archives
- Today
- Total
cyphen156
알고리듬 #10 적분으로 시간복잡도 구하기 본문
알고리듬 공부를 하다가 보면 흔히 그냥 시간복잡도는 그렇구나 근데 왜 그렇게 되지?에 대해선 별로 민감하지 않다.
나 또한 그렇다, 시간복잡도가 그냥 대충 절반씩 줄면 log단위겟구나, 반복문 중첩이 많을 수록 제곱 되는구나 식으로 넘어갔지
O(Nlog(logN))과 같은 시간복잡도가 왜 나오는지에 대해 궁금하지 않았다.
이번 글에서는 이런 시간복잡도를 적분을 통해 구하는 방식에 대해 소개한다.
적분 : 연속된 구간의 면적(누적량) 구하기
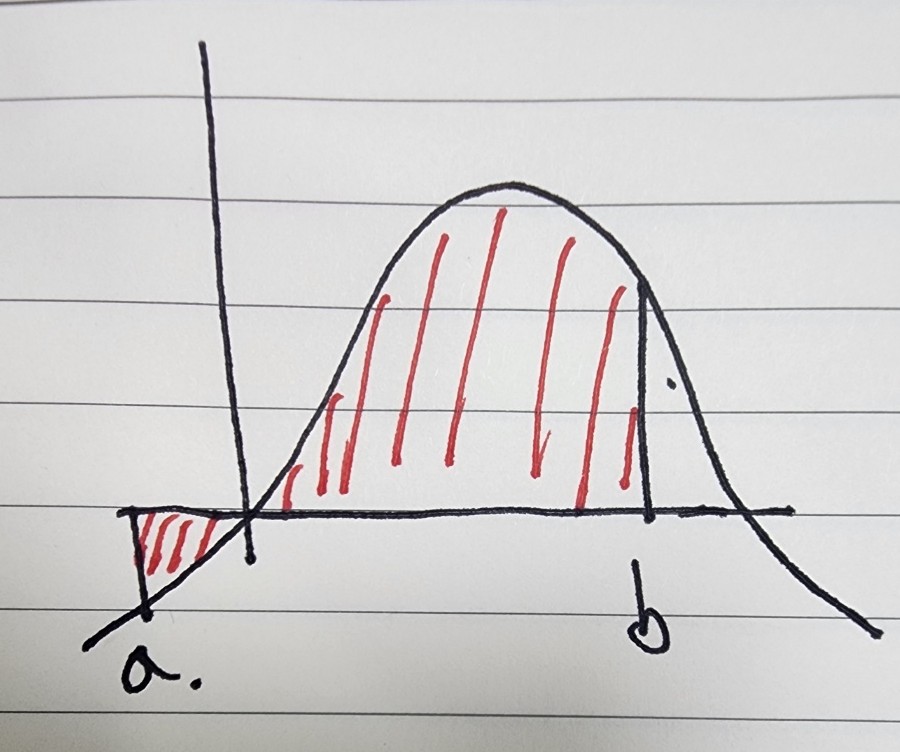
적분은 미분과 다르게 순간 변화율에 의해 실제로 변한 수치를 연속적으로 누적한 결과이다.
시간복잡도와 적분: 합을 면적으로 근사하기
보통 시간복잡도는 반복문의 총 비용을 다음과 같이 시그마를 통해 합으로 쓴다.
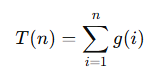
이 합을 막대들의 합(리만 합)으로 보고 곡선 y=g(x) 아래 면적(정적분) 으로 근사하면, 총 작업량의 차수(Θ) 를 빠르게 읽어낼 수 있다.
즉, 적분을 통해 면적을 구하는 것이 함수를 실행했을 때 발생하는 총 작업량을 구하는 것과 같아진다는 것이다.
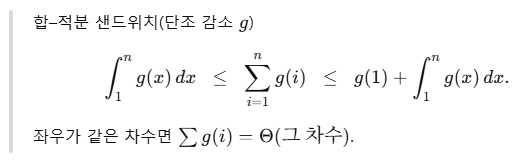
사실 이렇게 정리해놔도 아직 무슨 소리하는지 잘 모르겟다.
내가 지금 이해할 수 있는것은, 시간복잡도가 함수의 형태로 그려질 수 있고, 이것을 적분함으로써 시간복잡도를 근사해 그릴 수 있다는 아이디어가 사용된다는 것 정도일 것이다.
이 시간복잡도의 분석과 증명은 학계에서 해줄테니,
우리 개발자 입장에서는 "음 이런 원리로 이 함수를 쓰면 이정도 시간안에 문제를 해결 할 수 있겠구나"를 추측하고 효과적으로 사용할 수 있는 것 정도로 받아들이면 될 것 같다.
다음은 지피티한테 설명해달라고한 에라토스테네스의 체의 시간복잡도이다.

'컴퓨터공학 > 알고리듬' 카테고리의 다른 글
| 알고리듬 Extra #1 최단경로 구하기 : 다익스트라를 일부만 정렬해서 최단거리 구하기 (0) | 2025.09.17 |
|---|---|
| 알고리듬 #9 뉴턴법과 근사해 : 미분·적분으로 수치 계산해보기 (0) | 2025.09.16 |
| 알고리듬 #8 누적합과 계차 : 효과적으로 수열 다루기 (0) | 2025.09.12 |
| 알고리듬 #7 계산 기하학 : 컴퓨터로 그림 그려서 문제 풀기 (0) | 2025.09.12 |
| 알고리듬 #6 점화식과 동적계획법 : 규칙 찾아내기 (0) | 2025.09.11 |




